問 題
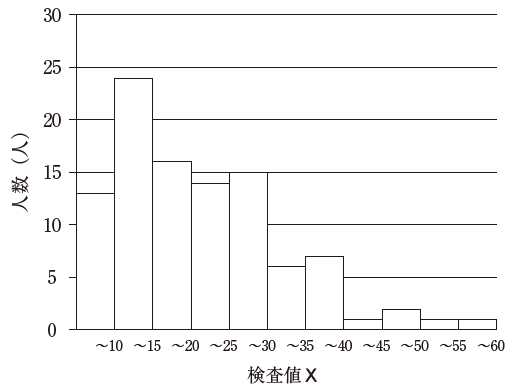
被験者 100 人について、ある臨床検査値 X を調べた時のヒストグラムが以下のようになった。同じデータに基づいて作成した箱ひげ図として、妥当なのはどれか。1 つ選べ。
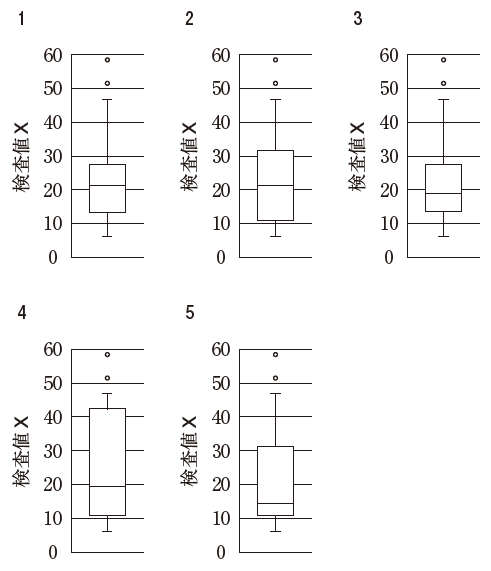
解 説
まず、箱ひげ図について基礎知識をまとめておきます。箱ひげ図からは「最小、最大、第一四分位数、中央値、第三四分位数」が読み取れます。
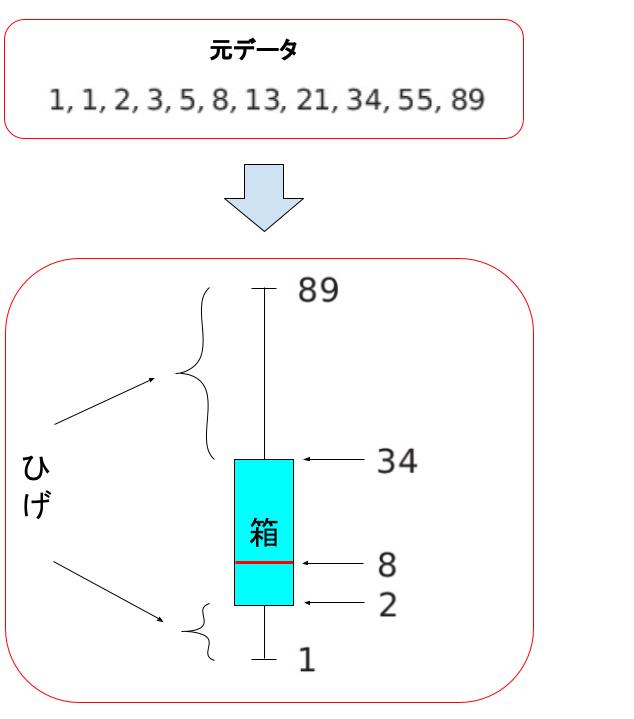
箱ひげ図の例として
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 という 11 個のデータを考えます。この 11 個のデータについて、最小は1、最大は 89 です。
中央値(メディアン)は、小さい方からデータを並べた真ん中の値です。例のデータでは「8」です。中央値よりも小さい値が 1,1,2,3,5、中央値よりも大きい値が 13,21,34,55,89 となります。それぞれのデータの中でもう一度中央値をとると、「2」 と 「34」 です。これがそれぞれ、第一四分位数と第三四分位数になります。
まとめると
最小1,最大 89、第一四分位数 2、中央値 8、第三四分位数 34 です。これをもとに、箱ひげ図を描くと、以下のようになります。箱、ひげ とはどこか、どの部分とどの値が対応しているかに注目してください。
以上をふまえ、本問の選択肢に注目すると、最小 及び 最大値は同じです。第一四分位数、中央値、第三四分位数が選択肢によって異なっています。
被験者数が 100 人なので
大体 25 人目、50 人目、75 人目の値を読み取れば、第一四分位数、中央値、第三四分位数がほぼわかります。
ヒストグラムから、25 人目は、「10 ~ 15」の所に該当します。50 人目は、「15 ~ 20」の所に該当します。75 人目は、「25~30」の所に該当します。この値に該当する箱ひげ図は、選択肢 3 となります。
以上より、正解は 3 です。

コメント