問 題
1 ~ 6 の異なる数字が各面に一つずつ書かれた正六面体のサイコロを振って, 1 又は 2 の目が出たら 5 点加点し, 3 ~ 6 の目が出たら 3 点減点するゲームを行うとき,サイコロを 5 回振った時点の点数が 9 点である確率はいくらか。
ただし,ゲームは 0 点から開始するものとし,点数がマイナスになることもある。
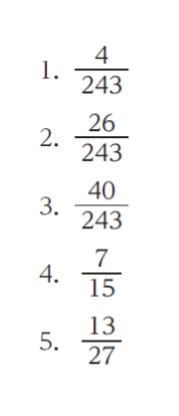
正解 (3)
解 説
まず、具体的に考えます。
サイコロを5回振って、全部1か2なら 25 点です。4回1か2で、1回3~6のどれかであれば 17 点です。9点となるのは「3回 1or2 、2回 3~6」という目の出方をした時であるとわかります。
「1 or 2 が出る」ことを「◯」で、「3 ~ 6 が出る」ことを「☓」と表します。◯の確率は 2/6 = 1/3 です。☓の確率は 4/6 = 2/3 です。
一例としては ◯◯◯☓☓ というパターンが考えられます。「☓が2回どこで出るか」は 5C2 = 10 通りのパターンが考えられます。(1回目~5回目の中で、1,2、1,3、1,4、1,5、2,3、2,4、2,5、3,4、3,5、4,5 回目 という 10 通りのパターンです。)
以上より、求める確率は

です。計算すると 40/243 となります。
以上より、正解は 3 です。

コメント