過去問 H30年 国家一般職（高卒 基礎）No.21解説

　問 題　　　　　

2 次関数 y= x² -x + 2 のグラフを x 軸方向に -2 ，y 軸方向に -2 だけ平行移動して得られる放物線が，直線 y = x + a と接するとき，a の値はいくらか。

1.  -1
2．1
3．3
4．5
5．7

 

 

 

 

 

　解 説　　　　　

平行移動や接する　という条件を式で計算するのは大変です。そこで具体的に 1点ずつ に注目するのがおすすめです。

まず、元の２次関数に適当に簡単な値を代入します。
x = 0 を代入すれば、y = 2 です。点 (0,2) は、-2,-2 平行移動すれば (-2,0) です。同様に、x = 1 を代入すれば、y = 2 です。-2,-2 平行移動すれば (-1,0) です。また、x = 2 を代入すれば、y = 4 です。-2,-2 平行移動すれば (0,2) です。３点がわかればグラフの概形がわかります。以下のようになります。

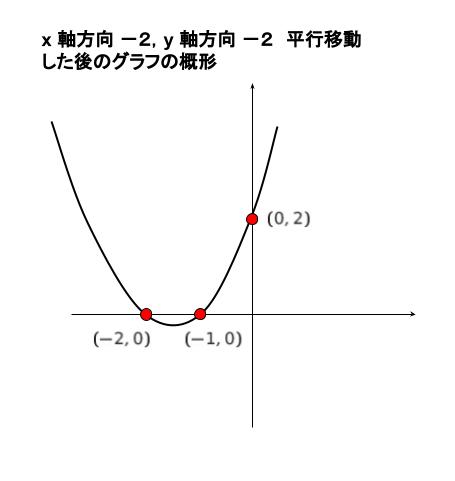
このような概形のグラフと、直線 y = x + a が接する時の a が聞かれています。選択肢を検討すれば、a = -1 の時は明らかに接しません。a = 3 より大きいと、明らかに 2 点と交わります。a = -1,及び a = 3 の時の概形が以下のようになります。

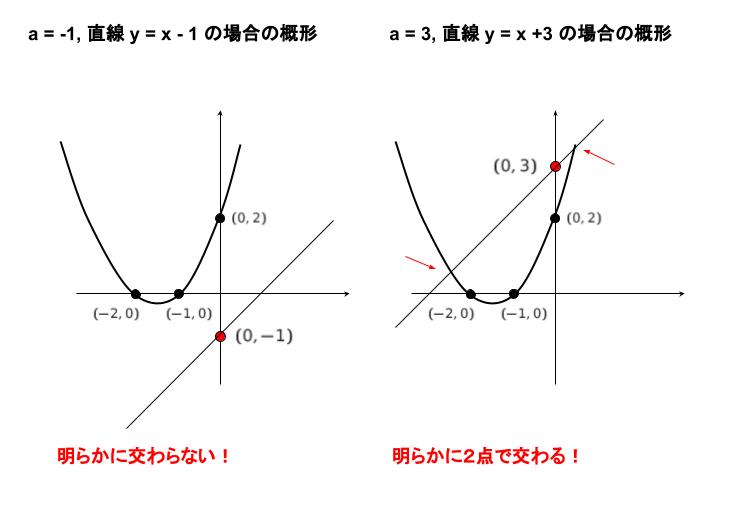
従って、a = 1 が求める答えです。

以上より、正解は 2 です。