問 題
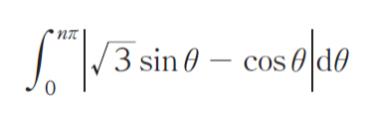
の値として正しいのはどれか。ただし,n は正の整数とする。

正解 (5)
解 説
n = 1 の場合を考えます。2つの解法をあげます。馴染みやすい方を優先して身につけるとよいと思います。
【解法1 定積分】
sin を積分したら -cos、cos を積分したら sin です。これは基礎知識です。θ = 0°、π(180°) の時の|√3sinθーcos θ| の値は、共に1です。 |√3sinθーcos θ| の値がちょうど 0 になるのは、有名角を考えれば θ = 30°(= π/6)とわかります。具体的な点をつなぐことで、グラフの概形は以下のようになります。
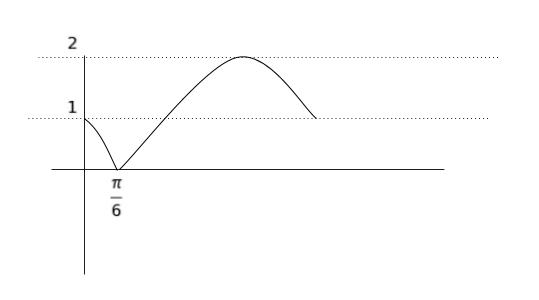
θ = 0~π/6 と、 θ = π/6 ~ π までに分けて積分します。


両方合わせて(2ー√3)+(2+√3)= 4です。正解は 5 です。
【解法2 合成】
三角関数の合成より、√3sinθーcosθ = 2sin(θ-30°)です。sin の一山が 2 なので、2 倍して 4 です。
以上より、正解は 5 です。

コメント