公務員試験 H30年 国家一般職(行政) No.34解説

　問 題　　　　　

ある製品を生産する企業が二つの工場を保有しており，それぞれの工場における費用関数は

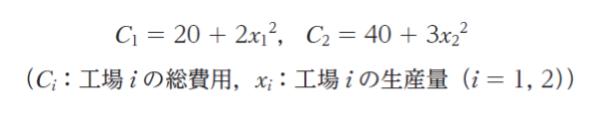
で示される。

完全競争市場における製品の価格が360 であるとき，この企業の利潤が最大となるときの，各工場の生産量 x₁，x₂ の組合せとして妥当なのはどれか。

　　x₁　  x₂
1． 50　  100
2． 90　  60
3． 120　240
4． 150　100
5． 200　160

 

 

 

 

 

　解 説　　　　　

添字が少し面倒なので、x₁ = x、x₂ = y とおきます。

製品の価格が 360 なので、企業の売上は 360 × (x + y) です。利潤は、売上ー費用なので、360 ×(x + y) ー(C₁ + C₂) = 360 × (x + y) ー(20 + 2x² + 40 + 3y²) です。従って、f(x,y) = 360(x + y) -(2x² + 3y² + 60) の最大値を求める問題 といい変えることができます。

2 変数関数なので、1 文字に注目し、x のみを変数と考えて、x で微分します。x で微分する、ということを df(x,y)/dx と表します。x を変数としているため、 360y、-3y² も定数項であり、微分すると 0 になる点に注意して計算します。df(x,y)/dx = ー4x + 360 です。 = 0 となる時は、x = 90 とわかります。これで答えは 2 とわかりました。一応確認のために、続きを計算しますが、本番ではここまでで十分です。

x = 90 を代入すると、f(y) = 360 (90+y) – (16200 + 3y² + 60) です。この関数の最大値を求めるために y で微分すると、df(y)/dy = -6y + 360 です。 = 0 となる時は、y = 60 とわかります。したがって、利潤最大となるのは、(x,y) = (90,60) の時です。

以上より、正解は 2 です。