問 題
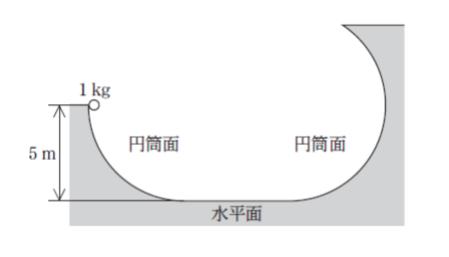
図のように,同じ半径をもつ滑らかな二つの円筒面と滑らかな水平面を,それぞれ滑らかにつなげた面上において,水平面から高さ5 m の円筒面上の点より質量1 kg の小球を静かに放したところ,小球は,円筒面を下り,水平面を通って,もう一方の円筒面を上った。
このとき,エネルギー保存の法則を用いると,小球が達する水平面からの高さの最大値はおよそいくらか。
1. 4 m
2. 5 m
3. 6 m
4. 7 m
5. 8 m
正解 (2)
解 説
水平面が滑らかで、エネルギーは失われないから、同じ高さまで上ります。よって、5mです。
あっさり 5m と出すのが少し不安な場合は、エネルギーを追っていくとよいと思います。まず、力学的エネルギー = 位置エネルギー+運動エネルギーです。これは摩擦力などが働かない限り保存されます。
位置エネルギー U = mgh です。
初めの状態において、U = 1 × g × 5 = 5g です。運動エネルギーはありません。
水平面に到達すると、位置エネルギーは0です。もともと有していた位置エネルギーは、全て 運動エネルギーとなっています。運動エネルギー K = mv2/2 です。 5g = v2/2 です。g = 10 とすれば、 v2 = 100 で v = 10m/s とわかります。
円筒面を上っていって、運動が止まり、運動エネルギーを全て失った時、位置エネルギーは 5g です。U = mgh で、m = 1 なので、U = 5g なら、h = 5 です。つまり、達する高さは 5m とわかります。
以上より、正解は 2 です。
類題 H29no54

コメント