問 題
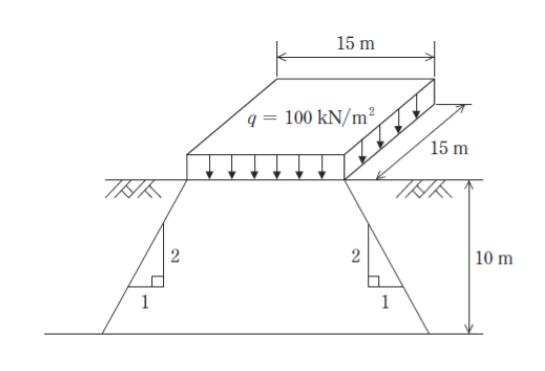
図のような一辺 15 m 四方の等分布荷重 q が地表面に作用したとき、深さ 10 m における地盤内鉛直方向の増加応力を近似計算法を用いて求めるとおよそいくらか。
ただし、図のように、載荷重による応力は載荷面の縁から一定の勾配で一様に分散するものとする。
1. 12 kN/m2
2. 24 kN/m2
3. 36 kN/m2
4. 48 kN/m2
5. 60 kN/m2
正解 (3)
解 説
100 kN/m2 の圧力を加えたんだから、増加分は 100 kN/m2 の圧力かというとそうではなく、力がじわっと広がっていくため、面積が広がって圧力は小さくなるけどどれくらい小さくなるでしょう?という感じの問題です。
かかる力は 225 × 100 = 22500 kN です。
深さが 2m 下がると、横にそれぞれ 1m 広がっているから、両端で 2m 広がります。つまり、10m 下がると、一辺は 10m 大きくなります。
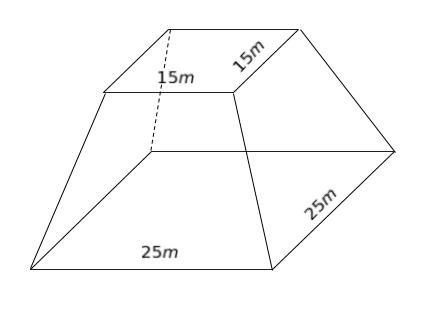
深さ 10m において、力が分布する面積は 25m 四方になるので、625m2 です。よって、増加分の応力は 22500 ÷ 625 = 36 です。
ちなみに、ボストンコード法として、「δZ = qBL/(B+2ztanα)(L+2ztanα)」と公式で覚えている人もいるかもしれません。本問において、B = L = 15、z = 10、tanα = 1/2 を代入すれば、やはり 36 が導けます。
以上より、正解は 3 です。

コメント