問 題
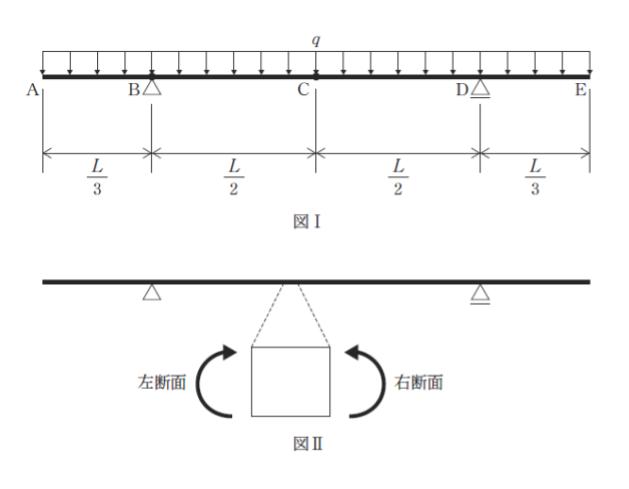
図Ⅰのような梁に等分布荷重 q が作用するとき,点 B 及び点 C の曲げモーメントの組合せとして最も妥当なのはどれか。
ただし,梁の自重は無視できるものとし,曲げモーメントは図Ⅱの向きを正とする。
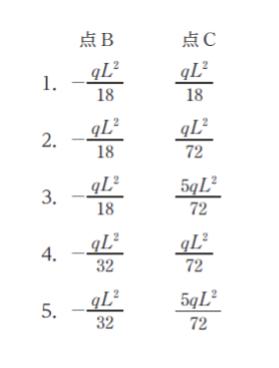
正解 (3)
解 説
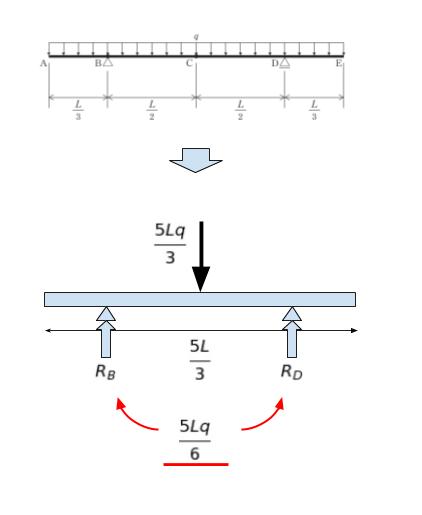
まず反力を求めます。反力を求める時に等分布荷重をいったん集中荷重に直して考えます。全長は 5L/3 なので、集中荷重は点 C に 5qL/3 かかります。点 B,点 D における垂直方向反力は、対称性から共に 5qL/6 と考えられます。
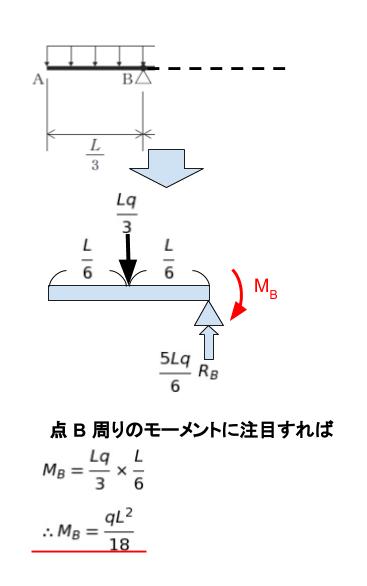
点 B における曲げモーメントを求めるために、図Ⅰにおいて、点 B で仮想切断し、左側を考えます。AB 間の等分布荷重を集中荷重に直すと、左から L/6 の所に qL/3 かかります。
モーメントは「力×距離」なので、この集中荷重により L/6 × qL/3 = qL2/18 のモーメントがかかります。従って、点 B 周りで考えれば、点 B に qL2/18 の曲げモーメントがかかっているとわかります。正解は 1~3 です。
同様に点 C で切断して考えます。AC 間の等分布荷重を集中荷重に直すと、左から 5L/12 の所に 5qL/6 かかります。集中荷重によるモーメントと、反力によるモーメントの差が Mc なので、計算すると 5qL2/72 です。
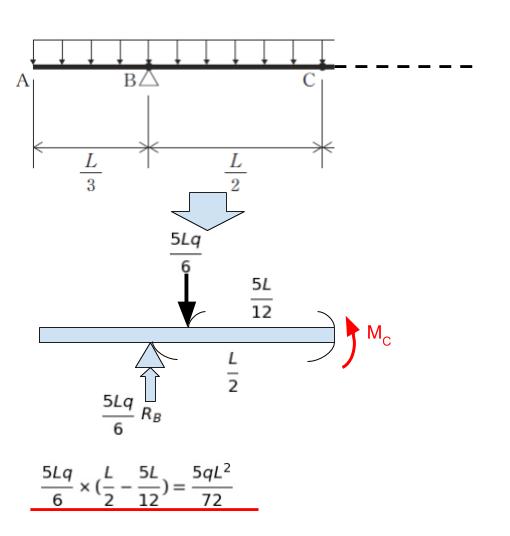
以上より、正解は 3 です。

コメント