問 題
光の回折と干渉に関する次の記述の㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。
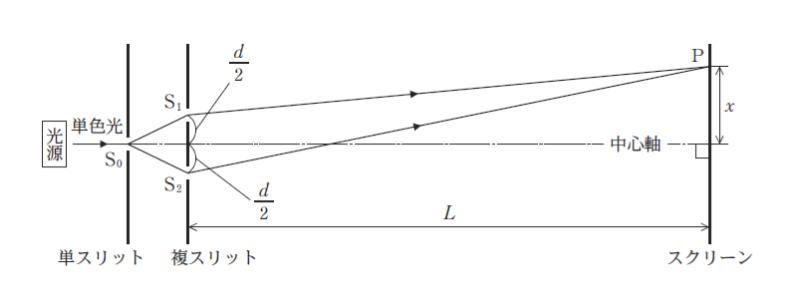
「図のように、単スリット S0、複スリット S1、S2、スクリーンを平行に置き、光源から S0 に向けて波長 m の単色光を照射したところ、スクリーン上に明暗の縞模様(干渉縞)が観察された。
複スリットとスクリーン間の距離は L である。また、光源を通りスクリーンに垂直な直線を中心軸とすると、S0 は中心軸上にあり、S1 及び S2 は、中心軸から同じ距離 d/2 離れている。
スクリーン上で中心軸から距離 x 離れた点を P とする。d、x が L に比べて十分に小さいとき、距離 S1P、S2P の差の大きさは ㋐ と近似できることから、スクリーン上の隣り合う明線の間隔 Δx は ㋑ と表せる。
この実験を、赤色光と青色光でそれぞれ行い比較すると、Δx は ㋒ を用いたときの方が大きい。」

正解 (3)
解 説
㋐ですが、 d が 0 に近づけば、S1P、S2P は0に近づくはずです。よって、分子に d があるべきです。1~3が正解です。
光路差が 波長の整数倍である時、強めあって明線です。中心軸とスクリーンの交点がまず 光路差 0 で強め合います。次に明るい所は 光路差 xd/L = λ なので、 x = Lλ/d です。
波長が大きいほうが ㋑ の値は大きいので、赤色光(より長波長光。λ大。)を用いた方が Δx が大きいです。 これで正解は 3 とわかります。
ちなみに、光路差の近似は三平方の定理により2つの光路差を計算した後、(1+h)n≒ 1+nh により、以下のように計算します。

以上より、正解は 3 です。

コメント