問 題
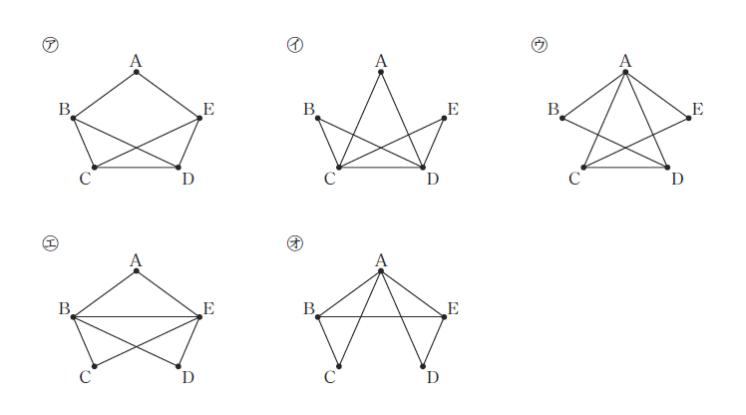
五つの頂点A~E をもつ次の㋐~㋔のグラフのうち,頂点A から出発し,全ての辺をそれぞれ一度だけ通って再び頂点A に戻れるもののみを全て挙げているのはどれか。なお,頂点は黒丸で示している点である。
1.㋐
2.㋐,㋒
3.㋑,㋒,㋔
4.㋑,㋓
5.㋓,㋔
正解 (4)
解 説
一筆書きの『途中の点』は「入ってきたら出ていく」はずだから、頂点から出ている線の数は偶数です。奇数の点は始点 もしくは終点にしかなりません。さらに始点かつ終点である点については、頂点から出ている線の数がやはり偶数になります。
以上をまとめると、一筆書きができる図形は、奇点が0 or 2 です。(オイラーの定理)。そして、奇点が2つの場合、その2つが始点及び終点です。従って、全部偶点である図形が、本問において題意を満たすと考えられます。以上をふまえ、それぞれのグラフについて検討します。
㋐ですが
奇点が 4 つ(B,C,D,E)なので、一筆書きができません。よって☓です。
㋑ですが
全て偶点なのでOKです。一例としてはA→C→B→D→E→C→D→Aでいけます。
㋒ですが
頂点 C,D が奇点なので、この2つが始点及び終点でないと一筆書きできません。ここまでの検討で選択肢より、㋑、㋓が妥当です。ちなみに㋓において、A→B→C→E→D→B→E→A が一例としてあげられます。
以上より、正解は 4 です。

コメント