公務員試験 H30年 国家一般職(電気・電子・情報) No.21解説

　問 題　　　　　

影像法に関する次の記述の㋐，㋑に当てはまるものの組合せとして最も妥当なのはどれか。

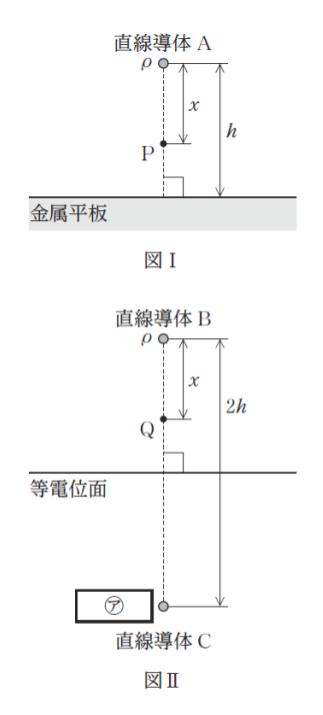
「図Ⅰのように，真空中に，無限に広い金属平板が水平に置かれており，単位長さ当たり ρ（ρ ＞ 0）電荷を与えた細い直線導体 A が，金属平板と平行に距離 h 離れて置かれている。A から鉛直下向きに距離 x（0 < x < h）離れた点 P の電界の大きさ E_P を影像法により求める。

図Ⅱのように，真空中に， 2 本の細い直線導体 B，C が，それぞれ，単位長さ当たり ρ， ㋐ の電荷が与えられて 2h 隔てて平行に置かれているとき，B，C から等距離にある面は等電位面になり，電気力線はこの面を垂直に貫く。したがって，B から C の向きに距離 x（0 < x < h）離れた点 Q の電界の大きさ E_Q は，E_P と等しくなる。よって，E_P を求めるためには E_Q を求めればよく，真空の誘電率を ε₀ とおけば，E_P = E_Q = ρ/2πε₀ (㋑) となる。

 

 

 

 

 

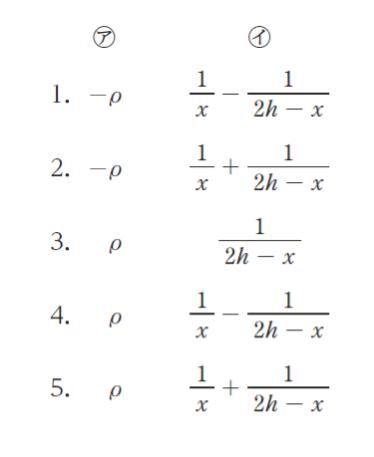
　解 説　　　　　

電気力線は「正→負」電荷へ向かう線として描きます。 問題文にあるように「B,C から等距離にある面を垂直に電気力線が貫く」のであれば、C は－の電荷と考えられます。よって、㋐はーρです。正解は 1 or 2 です。

「十分長い直線導体」から距離 a における電場の「大きさ」は E = ρ/2πε₀a です。そして、電場の「向き」は、＋１C の電気量を持った点電荷を置いた時の静電気力の向きといえます。直線導体 B からは、同符号なので斥力を、直線導体 C からは異符号なので引力を受けて、それぞれの導体が作る電場の向きは同じとわかります。よって、E_Q は、それぞれの直線導体が作る電場の大きさを「足したもの」です。

以上より、正解は 2 です。