問 題
ある会社では,同社の製品A,Bを製造する工場を新設することとなった。製品A,Bの製造ライン1 本当たり,設置に必要なスペースと作業員数,得られる利益は常に表のとおりであるとする。
これらの製造に割り当てることができるスペースは最大で 9,000 m2 であり,作業員数は最大で 600 人である。
この工場が製品A,Bの製造で得られる利益を最大にするには,製品Aの製造ラインを何本にすればよいか。
1. 3 本
2. 6 本
3. 9 本
4. 12 本
5. 15 本
正解 (2)
解 説
選択肢 1 が正解と仮定すると A 3 本→ 900m2、120 人使って利益 +45 です。残りの資源が 8100m2、480 人なので、B 13 本までいけて 利益 +260 なので、合計+305 です。以下、同様に考えると、A 6 本の時に、B12 本で +330 となり、これが最大です。
一般的には、線形計画法の問題です。総合職志望なら、こちらで解けるようにしておきましょう!それ以外なら不要です。
A x 本、B y 本 の時、利益は 15x + 20yです。これを k と表します。
15x + 20y = k を変形すると y = -3x/4 + k/20 となります。
傾き ー3/4 の直線を、条件満たす範囲で考え、y 切片(k/20)が最大になれば、k も最大です。
条件は、本問では
0≦x≦15、0≦y≦15
300x+600y≦9000
40x + 30y ≦ 600 です。以下のように図示されます。
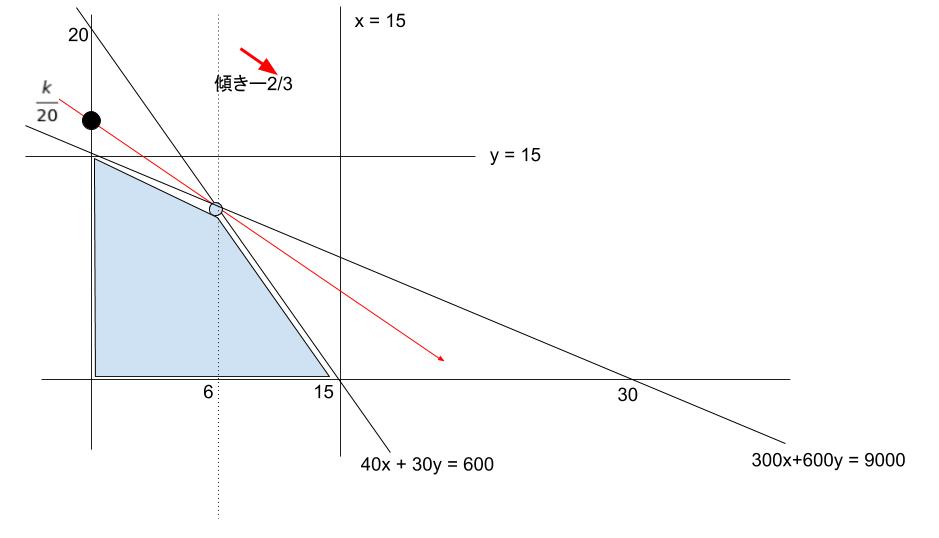
図より、x = 6,y = 12 の時最大となります。
以上より、正解は 2 です。

コメント