公務員試験 H29年 国家一般職(化学) No.14解説

　問 題　　　　　

反応速度に関する、次の記述の㋐、㋑に当てはまるものの組合せとして最も妥当なのはどれか。

「反応速度定数 k の温度依存性は次式によって表すことができる。この式はアレニウス式と呼ばれている。

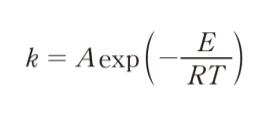
ここで、A は頻度因子、E は反応の活性化エネルギー、 R は気体定数、Tは絶対温度である。上式の両辺の対数をとると

 

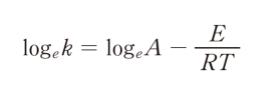
となる。

この式から活性化エネルギーが ( ㋐ ) なると、反応速度定数は温度に強く依存することが分かる。

360K における反応速度が 350K における反応速度の 2 倍となる反応があるとする。この反応の速度定数はアレニウス式で表すことができ、この反応の頻度因子及び活性化エネルギーは、温度によらず一定であるとすればこの反応の 400K における反応速度は 350K における反応速度の( ㋑ )倍となる。」
 
　　　㋐　　　　㋑
1．大きく　　2^3.5
2．大きく　　2^4.5
3．大きく　　2^5.5
4．小さく　　2^3.5
5．小さく　　2^5.5

 

 

 

 

 

　解 説　　　　　

㋐ ですが
具体的に E としてすごく小さい 0.001 と、すごく大きい 10000 を代入してみるとわかりやすいと思います。温度が 10K 変わった時に、E が 大きいほうが、より大きく数値が変動することが実感できるのではないでしょうか。従って、㋐は「大きく」が入ります。正解は 1~3 です。

㋑ について
まずは、350K,360K の場合について考えます。反応速度が 2 倍 というのは、反応速度定数が 2 倍　ということです。そこで、350K の時の k を k₁ とおきます。360K の時の k は 2k₁ とおくことができます。対数をとった式にそれぞれ代入してみて引き算することで　以下のような関係がわかります。※以下、 loge を ln と略しています。

T = 400K の時に反応速度が、T = 350K の時の a 倍になったとします。すると T = 400K の時の反応速度定数は「ak」と表すことができます。同様に式に代入して引き算をしてみれば

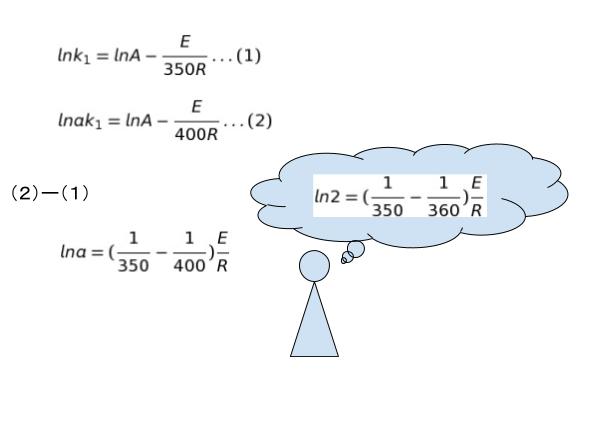
となります。

さきほどの引き算の結果と比較すれば、結局（　）の中の定数部分が何倍になったのかがわかれば a が何かわかりそうです。

1/350 – 1/360 は 、通分して計算すれば
36/35・10・36 ー 35/36・10・35
=1/10・35・36　です。

一方、1/350 – 1/400 は、通分して計算すれば
8/5・7・10・8 ー 7/5・8・10・7
=1/5・7・8・10　です。

従って、定数部分での違いは「分母の 36 と 8 の部分」です。1/36 と 1/8 を比較すれば、通分すると2/72 と 9/72 なので、4.5 倍になっています。つまり、lna = ln2 × 4.5 とまとめることができます。ここで　ln 2^x = x × ln2 であることから、右辺は ln2^4.5 となります。a = 2^4.5 です。

以上より、正解は 2 です。