公務員試験 H29年 国家一般職(行政) No.35解説

　問 題　　　　　

ある企業が独占的にある財を供給しているとする。この独占企業が直面している需要関数が，

Q = 60 – 2P　（Q：需要量，P：価格）

であるとする。また，この独占企業の総費用関数が，

C = X² + 6X + 8　（C：総費用，X：生産量）

であるとする。このとき，独占市場の均衡における総余剰の大きさはいくらか。

1． 16
2． 96
3． 112
4． 128
5． 208

 

 

 

 

 

　解 説　　　　　

独占市場なので、その１社は需要曲線を知っています。そして、利潤を最大化しようとします。独占ときたら、まずこの流れを思い出します。次の step は、利潤を問題文の式から求めることです。

Q = 60 – 2p を、p について解けば、p = -Q/2 + 30 です。生産量を X とおくと「p × X」が売上です。生産量 X と需要量 Q を一致させるように生産すると考えられるため、以降 Q = X として考えます。

利潤 ＝ 売上ー費用 です。従って、利潤は (-X/2 + 30)X ー （X² + 6X + 8） です。式を整理すると、利潤は -3X²/2 +24X -8・・・（１） です。

利潤最大化する X を求めるために（１）を微分し、０となるような X を求めます。以下のように計算を行い、X = 8 とわかります。この時、X = Q なので、Q = 8 です。代入すれば、p = 26 となります。

次に総余剰の大きさを考えます。需要曲線と限界費用曲線をグラフにして表します。限界費用曲線とは、総費用関数を微分したものです。総費用関数が問題文より C = X² + 6X + 8 なので、限界費用曲線 MC = 2X + 6 です。下図のように表すことができます。

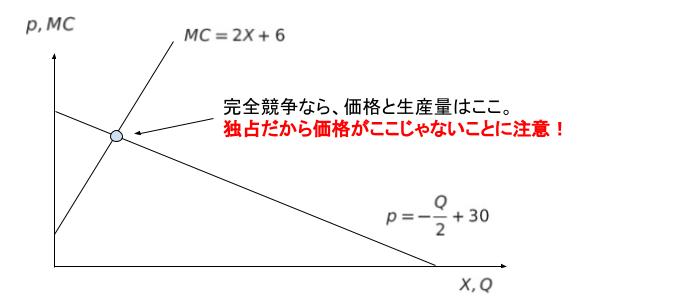
実際の価格は p = 26 で、 生産量 X = 8 でした。従って、X = 8 をグラフに書き込み、現れた台形部分の面積が総余剰となります。

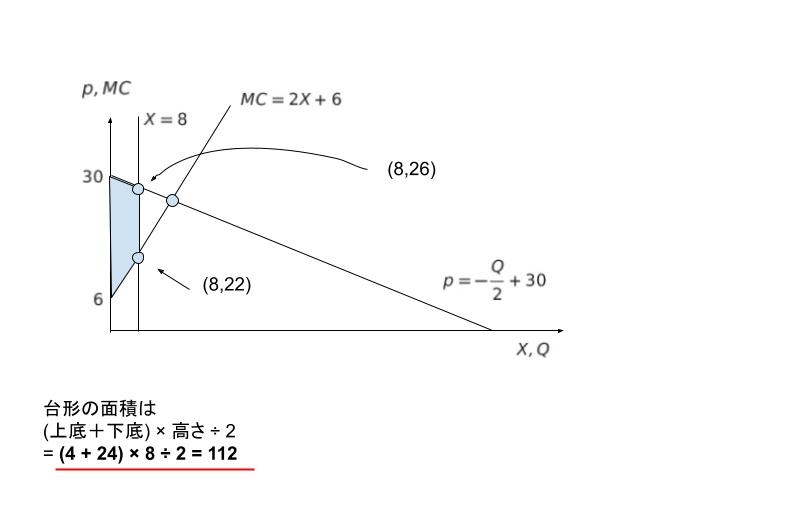
以上より、正解は 3 です。