問 題
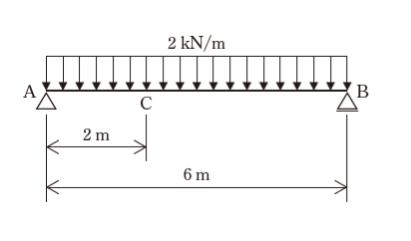
図のような等分布荷重を受ける単純梁において,点C における曲げモーメントMC の大きさはおよそいくらか。ただし,部材の自重は無視するものとする。
1. 4 kN・m
2. 6 kN・m
3. 8 kN・m
4. 10 kN・m
5. 12 kN・m
正解 (3)
解 説
まず反力を求めます。
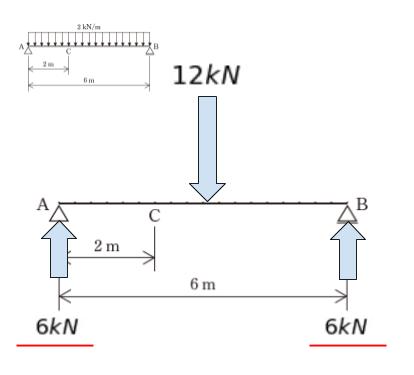
反力を求める時は、等分布荷重を集中荷重に直して考えます。 2kN/m × 6 = 12kN です。真ん中に集中荷重 12kN がかかっている梁と考えます。すると垂直方向の反力 RA、RB は対称性から明らかに それぞれ 6kN です。
求めるのは、点 C における曲げモーメント Mc です。点 C で仮想切断して、左側に注目します。AC間の等分布荷重を集中荷重になおすと 2kN/m × 2 = 4kN です。これが 点 A から 1m の所にかかっているという図で考えます。
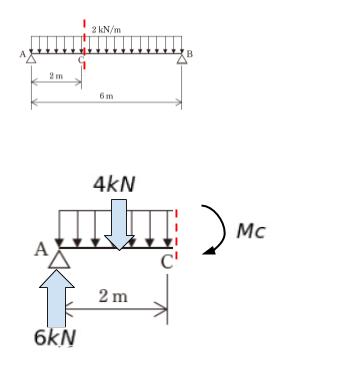
点 C 周りのモーメントを考えれば
4kN の力により 4 × 1 = 4kN・m(反時計回り)
6kN の力により 6 × 2 = 12kN・m(時計回り)です。
モーメントの和が 0 でなければならないため
Mc が 反時計回り 8kN・m とわかります。
以上より、正解は 3 です。

コメント