問 題
エネルギー保存の法則に関する次の記述の㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。
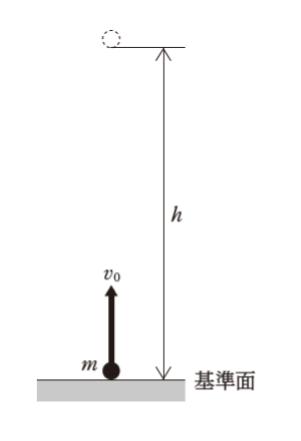
「図のように、床から質量 m の小球を鉛直上向きに速さ v0 で投げ上げたところ、小球は床から高さ h のところで最高点に達したとする。このときの h をエネルギー保存の法則から求めることを考える。
ただし、位置エネルギーの基準面を床にとり、重力加速度の大きさを g とする。
投げ上げた直後の小球の運動エネルギーは ㋐、位置エネルギーは 0(ゼロ)である。また、小球が最高点に達したとき、小球の速さは 0(ゼロ)であるから、運動エネルギーは 0(ゼロ)、位置エネルギーは ㋑ である。
エネルギー保存の法則より、運動エネルギーと位置エネルギーの和は、投げ上げた直後と最高点に達したときで等しいから、h は㋒となる。」
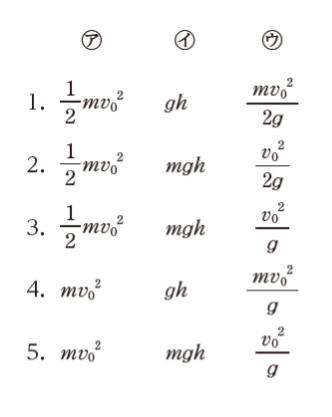
正解 (2)
解 説
力学的エネルギー=位置エネルギー+運動エネルギー が成立します。
ここで、重力による位置エネルギー U = mgh です。また、運動エネルギー K = mv2/2 です。これは基礎知識です。
㋐ですが、投げ上げた直後の運動エネルギーは 質量 m、速さ v0 なので mv02/2 です。
㋑ですが、位置エネルギーは mgh です。
力学的エネルギー保存より
mv02/2 = mgh です。h についてとけば
h = v02/2g です。(初速のみで、ボールの質量によらず最高到達点が決まる、ということです。さらにその高さは、初速を 2 乗し、大体 20 で割れば概算できるということを示しています。)
以上より、正解は 2 です。

コメント