問 題
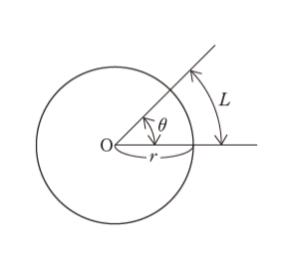
180° を rad(ラジアン)で表すといくらか。
なお、1 rad は、円弧の長さ L が半径 r と等しくなる角度で、図のように中心角 θ 〔rad〕、半径 r、円弧の長さ L をとると、これらの間には
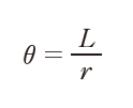
の関係が成り立つ。
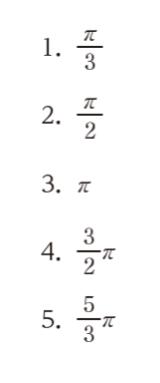
正解 (3)
解 説
π ラジアン = 180° です。これは基礎知識です。
忘れていた場合は問題文の「1 rad が、L と r が等しくなる角度」という所から導くとよいです。
半径 r → 直径 2r → 円周が 2πr です。中心角が もしも 1 °なら、円弧の長さは 1/360 × 2πr です。中心角が 2° なら、円弧の長さは 2/360 × 2πr です。中心角が x° とすると 円弧の長さは 「x/360 × 2πr」 と表すことができます。
これが r と等しい時、x = 180/π です。この角度が 1 rad です。
つまり 1 rad = 180/π ° なので、両辺に π をかければ
π rad = 180° です。
以上より、正解は 3 です。

コメント