問 題
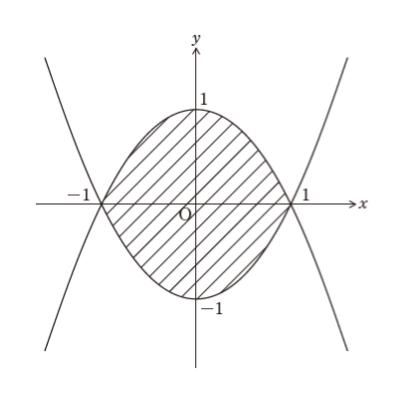
図のような,xy 平面上において曲線 y = -x2 + 1 と曲線 y = x2 – 1 で囲まれた領域の面積はいくらか。
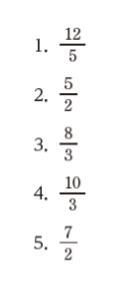
正解 (3)
解 説
【面積の概算】
明らかに斜線部は面積 1/2 の三角形 4 つ分より 大きい面積と概算できます。さらにはみ出す部分についても 2個で 1/2 よりは小さいだろうと考えられ、はみ出す部分 4 個 で最低 1/2 は超えそうです。以上から、面積 2.5~3 と当たりをつけることができます。すると正解は 3 です。
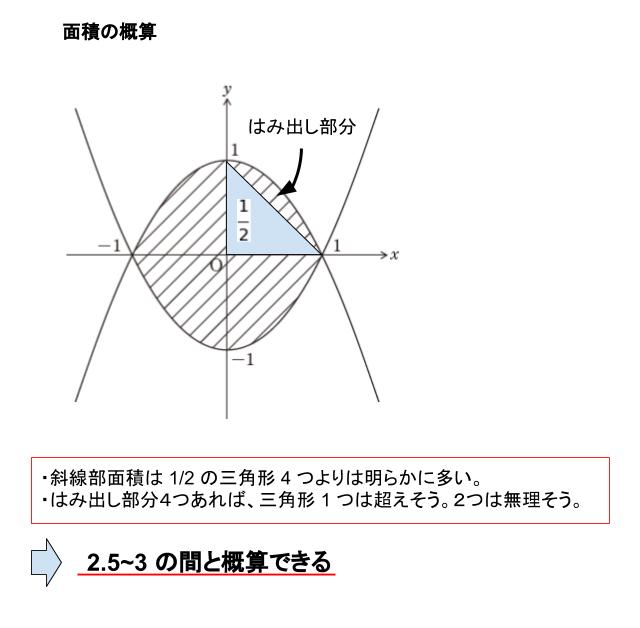
一応これで正解は 3 と推測されます。以下、確認のため定積分で計算しています。時間がない場合、これで決めうってもいいと思います。
【定積分による面積計算】
対称性から、x = 0~1 の部分の面積を計算して2倍すればOKです。
斜線部は x = 0 ~ 1 において、上端は y = -x2 + 1 、下端は y = x2 – 1 に挟まれた部分です。このような部分の面積は ∫ (上ー下)の 定積分で計算することができます。
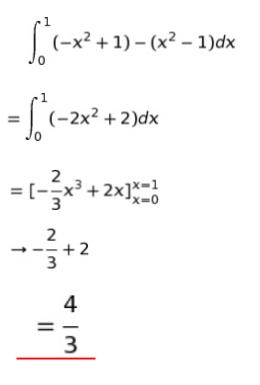
2倍すると 8/3 です。
以上より、正解は 3 です。
類題 H28no8

コメント