問 題
cosθ = -3/4 (0° ≦ θ ≦ 180°) のとき、sinθ、tanθ の値の組合せとして正しいのはどれか。
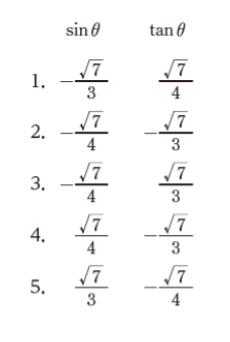
正解 (4)
解 説
θ が 90° を超えているため「単位円を用いた三角比の定義」を思い出します。単位円(半径 1 の円)を考えて、原点から θ 方向にビームを放ち、単位円との交点の x 座標、y 座標をそれぞれ x,y とします。この x 座標が cos θ、y 座標が sin θ です。
ちなみにこの時、tan θ = y/x です。本問では cos θ = -3/4 という条件が与えられていることを忘れないようにしましょう。
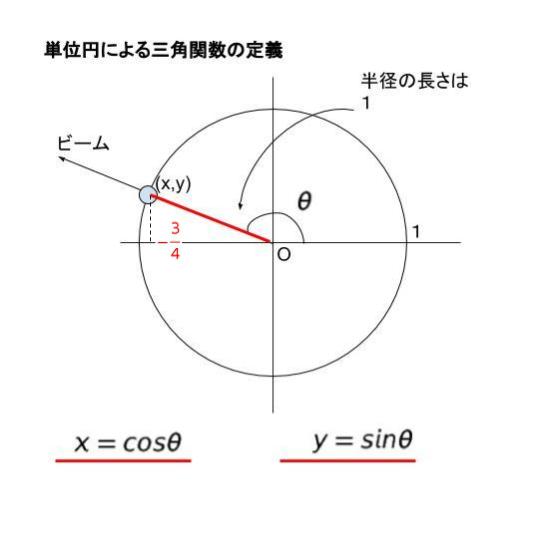
直角三角形の斜辺が 1、一辺の長さが 3/4 なので、三平方の定理より残りの一辺(sinθ)を求めることができます。(3/4)2 + sin2θ = 1 です。
※sin2θ + cos2θ = 1 という三角関数の基礎知識から、すぐに sin θ を求めてもかまいません。
※図から明らかに、y > 0 です。
選択肢より検討すれば、sin θ = √7/4 です。
tan θ は、sinθ/cosθ です。
ただ、本問では選択肢を見れば、sin θ = √7/4 の時点で正解がわかるため、tanθ を求める必要はありません。
以上より、正解は 4 です。
類題H28no4

コメント