H29年 国家一般職(高卒 技術) No.2 数学　解説

　問 題　　　　　

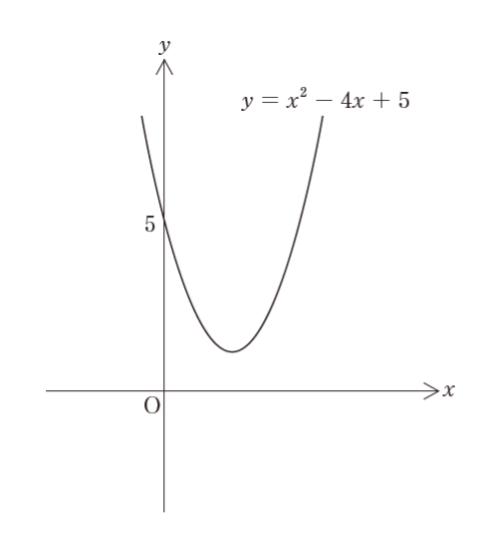
図のような曲線 y = x² – 4x + 5 を x  軸に関して対称移動して得られる曲線として正しいのはどれか。

1．y = -x² – 4x – 5
2．y = -x² + 4x – 5
3．y = -x² + 4x + 5
4．y = x² – 4x – 5
5．y = x² + 4x + 5

 

 

 

 

 

　解 説　　　　　

グラフ全体を一気に対称移動するのは難しいので、一点に注目して対称移動する、と考えるとわかりやすいかと思います。

まず、グラフから (0,5) を通っていることがわかります。この点を x 軸に関して対称移動すれば (0,-5) です。選択肢を検討すると、選択肢 3,5 は x = 0 を代入すると 5 になってしまうので誤りです。よって、正解は 1,2,4 のどれかです。

また
２次関数における特徴的な一点といえば頂点です。 頂点の x 座標が、y = ax² + bx + c の時、x = -b/2a です。これは基礎知識です。（忘れても、平方完成で導ければ OK です。）

今回は a = 1、b = -4 なので、頂点の x 座標は 2 です。 x = 2 を、y = x² -4x + 5 に代入すれば 4 – 8 + 5 = 1 です。これで頂点は (2,1) とわかります。

頂点を x 軸に関し対称移動すると (2,-1) に移動します。
x = 2 を代入すると
選択肢 1 は -17
選択肢 4 は -9 になるため誤りです。

以上より、正解は 2 です。