問 題
図のように水平面上を流れる流量Q、流速vの噴流が固定した壁面に斜め方向から衝突するとき、次の記述の㋐、㋑に当てはまるものの組合せとして最も妥当なのはどれか。
ただし、噴流は完全流体であり、壁面による摩擦損失はなく、衝突前の噴流の向きと壁面のなす角はθとする。
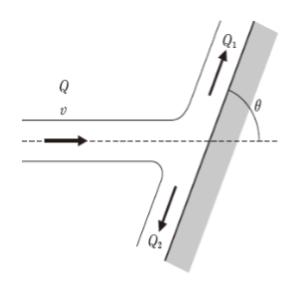
「完全流体の噴流の流速は、壁面への衝突前後で同じであり、壁面に平行な方向の運動量が衝突前後で保存されることから、
( ㋐ ) ……①
と表される。
また、連続の関係から、
Q=Q1+Q2 ……②
で表される。
式①、式②から、Q1は
Q1=( ㋑ )
と表される。」
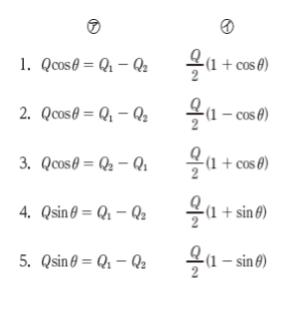
正解 (1)
解 説
θ = 90°の場合、きれいに左右(図的には上下)にわかれるから、Q1ーQ2 であろうがQ2ーQ1であろうが0 のはずです。
Q sinθ だと θ = 90°の時 1 となって左辺が 0 になりません。よって㋐の左辺は Q cosθです。
正解は 1~3 です。
Q cosθ = Q1ーQ2と仮定します。
Q = Q1+Q2と連立し、辺辺足してQ1 について解けば
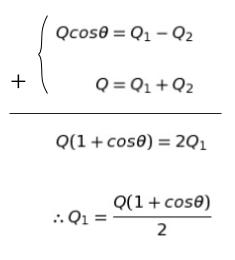
です。選択肢 2 は誤りです。
また、Qcosθ=Q2ーQ1だと符号が逆になるはずなので、選択肢 3 は誤りです。
以上より、正解は 1 です。

コメント