問 題
図Ⅰのように長さ8lの単純梁の両端の点a、点cにそれぞれ8Pl、3Plのモーメントが作用している。
このとき、点bにおけるせん断力と曲げモーメントの組合せとして最も妥当なのはどれか。
ただし、梁の自重は無視し、せん断力と曲げモーメントは図Ⅱの向きを正とする。
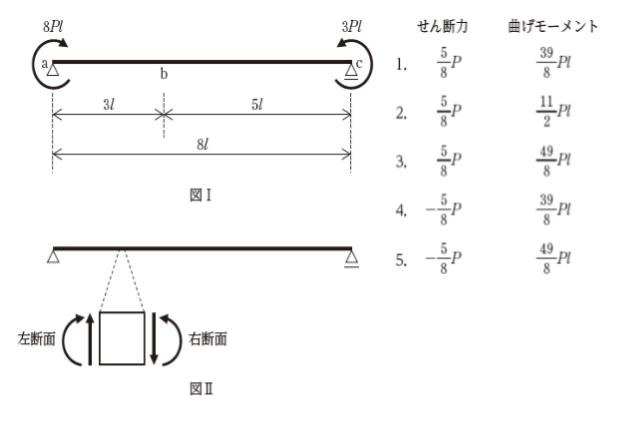
正解 (5)
解 説
支点反力をまず考えます。a点垂直反力を Ra、a点水平反力を Ha とします。c点垂直反力を Rc とします。
横方向の和が0に注目すれば、Haはすぐに0とわかります。(0なので下図にHa は書いていません。)
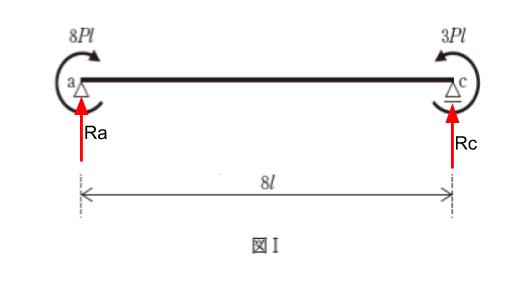
垂直反力を求めるために、a 点まわりのモーメントを考えます。支点なので和が0です。よって
8Pl = 3Pl + ( Rc × 8l ) が成立します。これを解くと、Rc = 5/8 P です。
縦方向の和が0なので、Ra + Rc = 0 です。従って
Ra = -5/8P です。力を書き込むと下図のようになります。
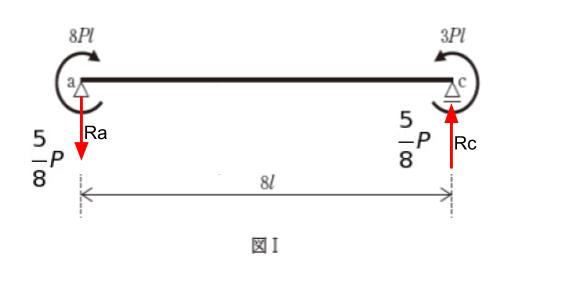
支点反力がわかったので、点 b におけるせん断力、モーメントをそれぞれ考えます。
点 b において仮想切断してみると、上向きに 5/8 P の力がかかるとわかります。「↓ ↑」のせん断力なので、符号は負です。
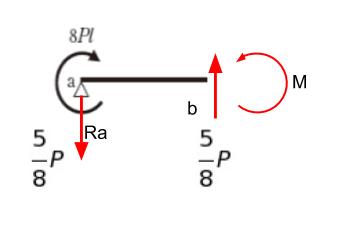
よって、正解は 4 or 5 です。
b 点まわりのモーメントを考えると
8Pl = (Ra × 3l) + Mb です。Ra = 5/8 P なので

となります。
以上より、正解は 5 です。

コメント