問 題
等式 7sinθ=3cos2θ(0≦θ<2π)を満たすθのうち最大のものをαとおく。このときのcosαの値として正しいのはどれか。
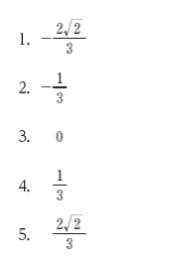
正解 (1)
解 説
cos2θ = 1-2sin2θ より等式は
7sinθ = 3(1-2sin2θ)
6sin2θ+7sinθ-3 = 0
(3sinθ-1)(2sinθ+3)=0
と変形できます。
∴sinθ = 1/3 です。
この時、sin2θ+cos2θ = 1 より
cosθ = ±2√2/3 です。
θ が大きいのは cos θ = -2√2/3 の時です。
※ここは注意が必要です!
(sinθ = 1/3,cosθ = 2√2/3となるようなθはずばっとわかりませんが、「sinθ,cosθが共に正」であることから少なくとも 0~90°の範囲です。
一方、sinθ = 1/3,cosθ = ー2√2/3 となるようなθは、やはりずばっとはわかりませんが90~180 の範囲となります。)
よって、正解は 1 です。

コメント