問 題
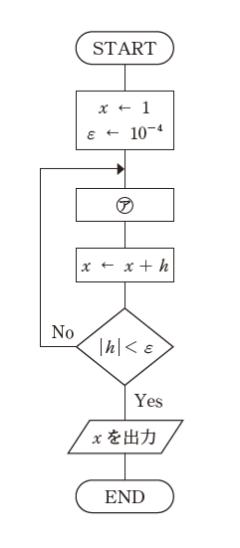
図は,方程式 cosx – x2 = 0 の解の近似値をニュートン法によって求めるためのフローチャートである。近似解の修正値 h の絶対値が f 未満になったときに,その近似解を出力して停止する。図中の ㋐ に当てはまるものとして最も妥当なのはどれか。
なお,ニュートン法は,関数 f(x) を近似解 xn のまわりにテイラー展開した下式について,左辺を 0 ,右辺第 3 項以下を 0 とした方程式の解を新たな近似解 xn+1 とし,繰り返し計算することにより,方程式 f(x) = 0 の解の近似値を求める方法である。

正解 (5)
解 説
問題文にある「下式について,左辺を 0 ,右辺第 3 項以下を 0 とした方程式の、、、」という記述を文字通り解釈します。本問での f(x) は cosx – x2 です。第 3 項以降 は 0 とのことなので、右辺は f(xn) + f’(xn)(x-xn) です。つまり

以上より、正解は 5 です。
類題 H25no35

コメント