公務員試験 H29年 国家一般職(電気・電子・情報) No.26解説

関数 f(t) が t ≧ 0 で定義されているとき，

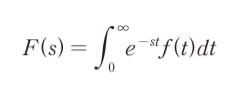
を f(t) のラプラス変換という。いま，f (t) = sinωt であるとき，そのラプラス変換として正しいのはどれか。

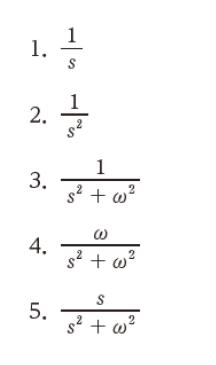
覚えていなかったら、定義に従い「e^-st sinωt 」を積分しますが、かなり計算が複雑なので これは知識問題ではないかと思われます。積分の指針としては、「指数関数×f(x) なので、部分積分」です。そして f(x) 部分が三角関数の場合は、まず全体をＩとでもおいて、２回部分積分をすることで元の形が出てきます。以下のようになります。

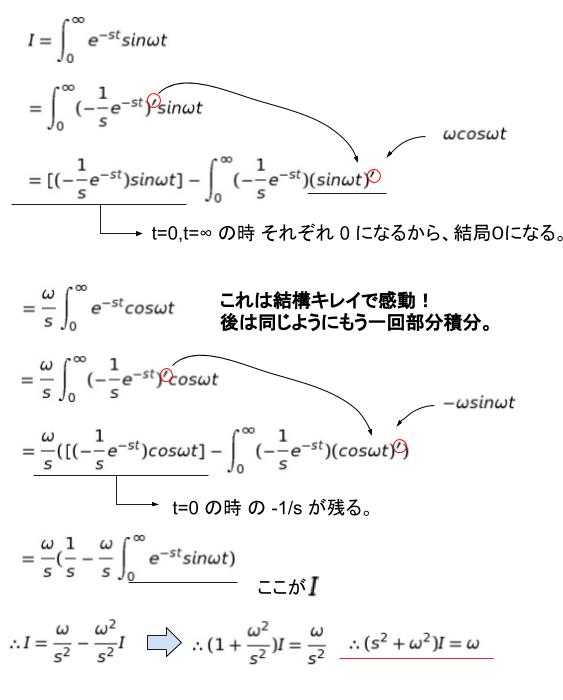
以上より、I = ω/(s² + ω²) です。正解は 4 です。
類題 H26no26