問 題
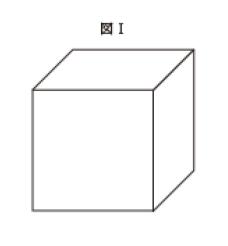
図Ⅰのような立方体に対し,隣り合う面どうし(一辺で接する面どうしを意味する。)が同じ色とならないよう塗り分ける。次に,立方体の各頂点について,図Ⅱのようにこの頂点を含む各辺の中点を通る平面で切り取る。
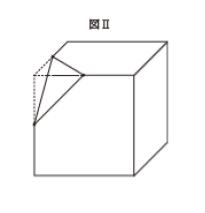
そして八隅を切り落として残った大きな立体を,隣り合う面どうしが同じ色とならないよう塗り分けた。このとき,この立体に塗られている色の数は最小でいくらか。ただし,一度塗った色は塗り直さないものとする。
1. 3
2. 4
3. 5
4. 6
5. 7
正解 (2)
解 説
展開図にすれば平面上における色分け問題です。平面における色分けは、最高でも4色で塗り分けることができます。(これは知識として持っておくとよいです。)
後は3色だと無理かどうかを考えればよいです。平面の4色について知らなくても、やはりできるだけ最小の色での塗り分けを考えるとよいです。
図Ⅰの立方体のある面に注目すると、その面は他の4面と接して、平行な1面とだけ接しません。そこで対面同士を同じ色にすると3色あれば塗り分けることができます。
隅を切っちゃうと、その隅は3色と接するはずだから、後1色必要です。隅同士は接さないから、4色で十分とわかります。
以上より、正解は 2 です。

コメント