問 題
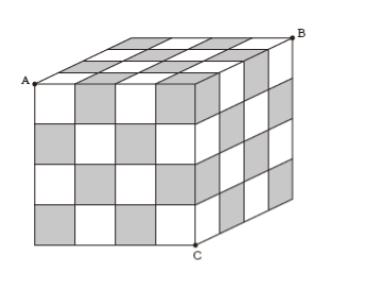
図のような,同じ大きさの白と黒の小立方体の計64 個を交互に積み上げて作った立方体がある。この立方体を,頂点A,B,Cを通る平面で切断するとき,切断される黒の小立方体の数はいくつか。
1. 6 個
2. 8 個
3. 10 個
4. 12 個
5. 14 個
正解 (1)
解 説
小さな立方体を積み上げた立方体の問題で、各小立方体について考える場合は「スライス法」です。スライス法とは、各段をスライスして切断し、1段ずつ考えていくことです。
スライス法で、まず一番上の段に注目し切断面を考えると、黒の小立方体は3つ切断されると考えられます。
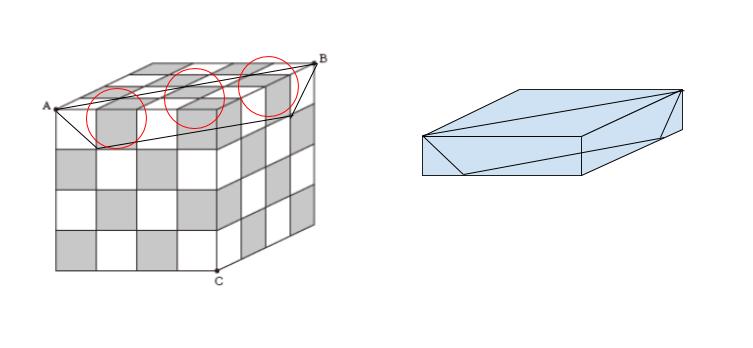
次の段は 3×3 の立方体に対して、全くさっきと同じ切断を試みると考えられるので、黒の小立方体は2つ切断されます。イメージが下図です。
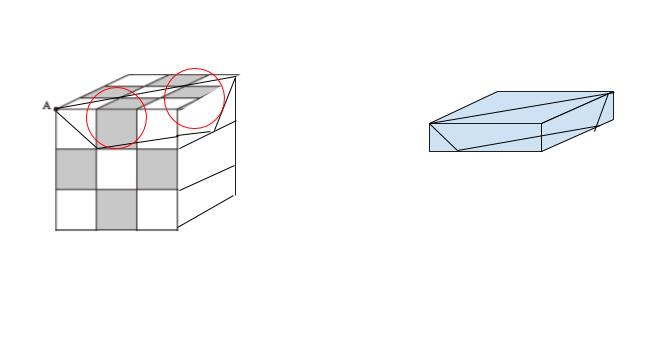
その次の段は2×2の立方体に対して、全くさっきと同じ切断を試みると考えられるので、1つ切断されます。で、最後は 0 です。よって、3+2+1=6です。
以上より、正解は 1 です。

コメント