問 題
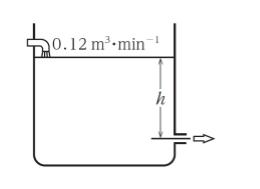
図のように水が入っている大きなタンクがある。タンクの下方側壁には面積 5.0cm2 の小孔がありそこから水が流出している。
このタンクに毎分 0.12m3 の水を緩やかに供給し続けたところ、水位が一定となった。このときの小孔の中心から水面までの高さ h はいくらか。
ただし、重力加速度の大きさを 10m・s-2、流量係数を 0.60 とし、タンクの断面積は小孔の面積に比べて十分大きいものとする。
1.1.6m
2.2.2m
3.4.5m
4.5.6m
5.7.7m
正解 (2)
解 説
小さい穴から流れる流量 Q が、ちょうど 0.12m3/分 と考えられます。重力加速度の単位が 秒が基準でさらに、面積は cm2 なのでまず、単位を変換しておきます。0.12m3/分 について、まずは 1分 = 60秒なので
0.12m3/分 = 0.002m3/sec = 2 × 10-3m3/sec です。
次に、1m3 = 106cm3 なので
2 × 10-3m3/sec = 2×103 cm3/sec です。
タンクで小さな穴なので、トリチェリの定理です。v = √2gH です。また、連続の式よりQ = Avです。ただし流量係数をかけます。
2×103 cm3/sec = 0.6 × 5.0 × √2gH が成立すると考えられます。※ただし g , 高さ H の単位は m でなく cm になおします。

以上より、選択肢を参考に、H = 2.2m です。正解は 2 です。

コメント