問 題
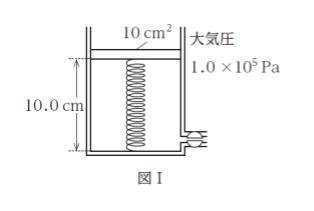
ばねに支えられている断面積 10cm2 のピストンが、コックと側管が付いたシリンダーに取り付けられている。図Ⅰのようにコックを開き、側管を大気に開いた状態でピストンに何も載せないとき、ピストンは底から 10.0 cm のところにあった。
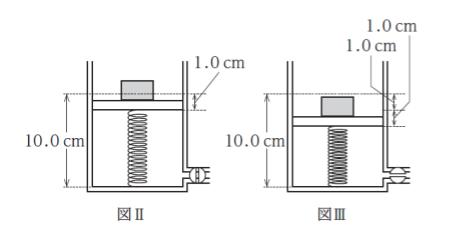
次に、コックを閉じ、ある質量のおもりをピストン上に載せたところシリンダー内の空気の温度が変化することなくピストンがゆっくりと下がり図Ⅱのように、1.0 cm下がって静止した。
さらに、図Ⅱの状態でコックを開いたところシリンダー内の空気の温度が変化することなくゆっくりとピストンが下がり図Ⅲのように、更に 1.0 cm 下がって静止した。おもりの質量はいくらか。
ただし、大気圧を 1.0×105 Pa重力加速度の大きさを10m・s-2としシリンダー内壁とピストンの間には摩擦はなくばね及びピストンの質量は無視できるものとする。
1.0.48kg
2.0.82kg
3.1.5kg
4.2.2kg
5.4.9kg
解 説
図Ⅰ→ 図Ⅱでは、ピストン内の体積が 100 cm3 → 90 cm3 と「V が 9/10 倍」になっています。「シリンダー内の温度が変化することなく」と強調されている点からも理想気体の状態方程式を思い出します。
PV = nRT より、V が 9/10 倍になったのであれば「P は 10/9 倍になった」と考えられます。変化したのは、大気圧の 1/9 倍分です。そして、図Ⅱ→図Ⅲではコックが開いたことにより増加していた圧力で支えていた分がなくなってその結果、さらにピストンは下へと押し下げられています。
ここでばねなので、フックの法則 F = kx を考えてみれば、x = F/k です。k は定数です。図Ⅰ → 図Ⅱ と、図Ⅱ → 図Ⅲ においてx、すなわちばねの変位が同じく 1.0cm です。つまり、図Ⅰ→図Ⅱ における変化した下向きの力と図Ⅱ→図Ⅲ における変化した下向きの力は「同じ」である とわかります。
これらをまとめると、図Ⅰ→図Ⅱでは「大気圧の 1/9 倍分」だけおもりで押し下げられ、図Ⅱ→図Ⅲでは図Ⅰ→図Ⅱ での変化分と同じだけさらに下向きに押し下げられたということです。従って「大気圧の 1/9 倍分 とつりあう質量のおもり」がわかれば、それを 2 倍すればこの問の答えです。
【解法1】
1Pa = 1N/m2(ここを覚えている前提とします。)
1 Pa = 1N/10000cm2(1m2 を cm2 になおします。)
1.0 × 105Pa = 100000N/10000cm2
1.0 × 105Pa = 100N/10cm2 です。
この圧力が 10/9 倍になったのなら、増加分が 1/9。100 × 1/9 ≒ 11.1N。F = mg で、g = 10 なので、m ≒ 1.1 kg。これを 2 倍すると答えなので、2.2 kg です。
【解法2】
「水圧だったら10mでちょうど大気圧の2倍」という知識を使って推測します。
1cm 四方の空間に、10m の水があればそれが大気圧分ということです。10m = 1000cm です。1cm 四方で高さ 10m ならば、その体積は ちょうど 1L です。水 1L は、1kg です。従って、「1cm2 に 1kg 乗ってれば大気圧」です。
となれば、1cm2 に 1×1/9 = 0.11kg をプラスすれば、大気圧の 10/9倍になるとわかります。10cm2 だったらその 10倍の 1.1kg をプラスすれば OKです。1.1kg のおもりをのせれば大気圧の 10/9 倍 とつりあいます。その 2 倍が答えなので 2.2kg です。
以上より、正解は 4 です。

コメント