問 題
電気回路に関する次の記述の ㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。
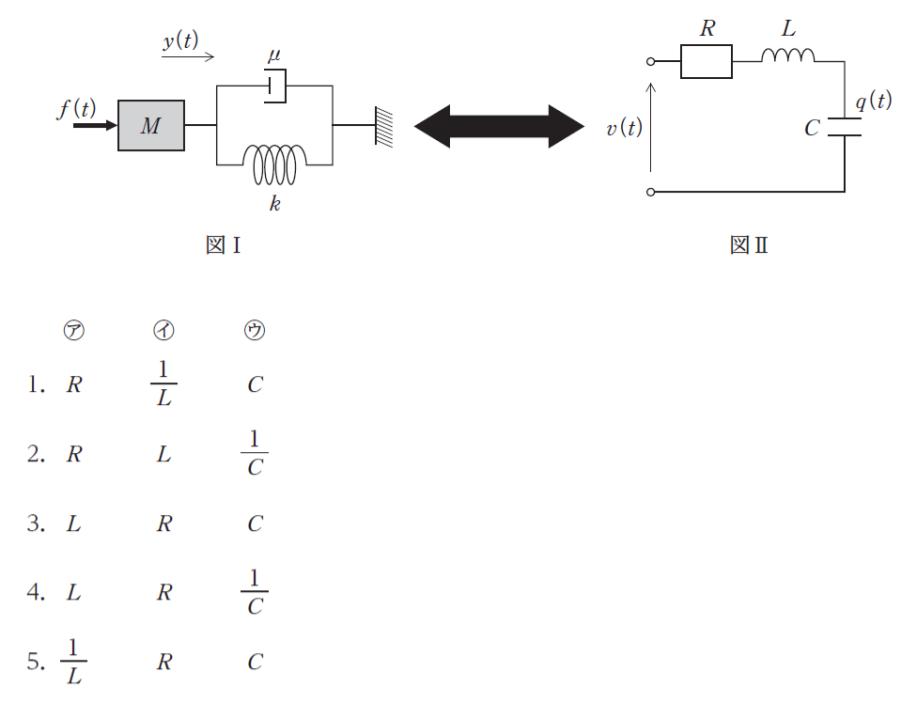
「図Ⅰに示す質量 M の物体、ばね定数 k のばね、粘性減衰係数 μ のダンパからなるモデルの運動方程式と、図Ⅱに示す抵抗値 R の抵抗インダクタンス、 L のコイル、静電容量 C のコンデンサからなる RLC 回路の回路方程式とは、同じ形の微分方程式で表される。
物体、ばね、ダンパからなるモデルの運動方程式は、時刻をt、加える力をf(t)、変位を y(t) とすると、速度は y'(t) 、加速度は y”(t) であるから
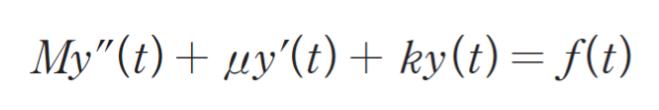
と表せる。
一方、RLC 回路の回路方程式は、時刻を t、加える電圧を v(t)、コンデンサに蓄えられる電荷を q(t) として同様に考えると
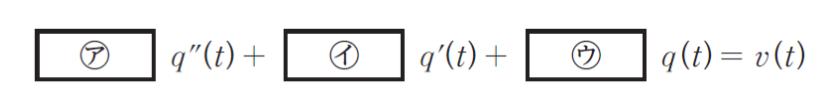
と表せる。」
正解 (4)
解 説
まず、抵抗 R に注目します。電圧降下は RI です。ここで類題より「I = dQ/dt」 と表されることを想起することが期待されていると考えられます。すると R と「q’(t)」 がセットと考えられるため、正解は 3~5 です。
さらにコンデンサの基本式 Q=CV より、V = Q/C です。よって、㋒ は 1/C と考えられます。
以上より、正解は 4 です。
ちなみにですが、コイルの電圧が、V = Ldi/dt と表されます。この i に dQ/dt を代入することで、q’’(t) と L がセットになります。
類題 H24no8

コメント