公務員試験 H28年 国家一般職(化学) No.4解説

　問 題　　　　　

五つの選択肢の中から、解答を一つ選ぶ問題が 40 題ある。Aさんは 20 題は完璧に解答できたが残りの問題は全然分からなかった。そのため、分からなかった問題については、無作為に一つの選択肢を選んで解答した。

完璧に解答できた 20 題については全て正答であったとすると、Aさんが全体で 25 題以上正答する確率を表す式として正しいのはどれか。ただし、各問題につき正答の選択肢は一つのみとする。

 

 

 

 

 

 

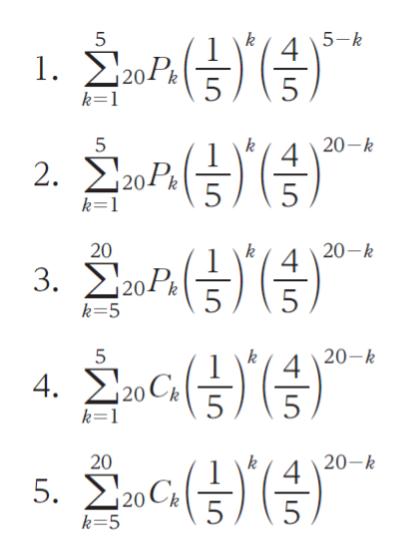
　解 説　　　　　

思いっきり今解いている公務員試験多肢試験についての問題ですね！本番で「何このメタな問題・・・」と話題になったのではないでしょうか。20 問確実に解けるってよく勉強してるなぁ。。。

本問は結局の所「ランダムに 5 択を 20 問解いて5/20 以上取れる確率を求めよ」という問題です。すると、5/20,6/20,7/20,,,20/20（！） までランダムで取れる可能性があるので、Σ を使って表されています。

ランダムに５問正解する　という場合を例に考えてみます。「○○○○○☓☓☓☓☓☓☓☓☓☓☓☓☓☓☓」なら 5 問正解です。この確率は、(⅕)⁵(⅘)¹⁵ と表せます。どの５問が偶然正解になるかという点に関して、「20問中５問の選び方」は「₂₀C₅」 です。従って「ランダムに５問正解する」確率は、₂₀C₅ (⅕)⁵(⅘)¹⁵ です。
（₂₀C₅ = 15504 なので、計算すると　大体 18% となります。）

以下
20問中 6 問なら、₂₀C₆ (⅕)⁶(⅘)¹⁴です。
20問中 k 問 (kは 5~20) なら、₂₀Ck (⅕)k(⅘)20-k です。k が５～２０までをすべて足せばよいので、Σ₂₀C_k (⅕)^k(⅘)^20-k（kは 5~20）です。

以上より、正解は 5 です。
 
ちなみに、２０問ランダムで解いて１問も当たらない確率は (⅘)²⁰ ですがこれって計算してみると約 1% なんですね。100人に解いてもらうと1 人ぐらい出るとなると、意外にあるんだな・・・と驚きました！