問 題
微分方程式
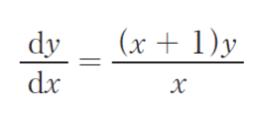
の解として正しいのはどれか。ただし、x = 1 のとき y = e とする。
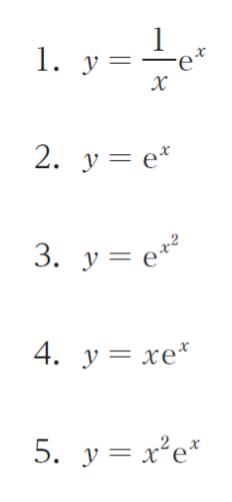
正解 (4)
解 説
dy/dx というのは y’ と同じ意味です。解は選択肢 1 ~ 5 のどれかなので正解を仮定して考えます。微分するのが簡単なものから考えるとよいです。
まず、y = ex(選択肢 2)が正解とします。y’ = ex です。微分方程式に代入してみると
左辺 = ex です。右辺 = (x+1)ex/x です。左辺≠右辺です。選択肢 2 は誤りです。
他の選択肢はどれも、積の微分をしなければいけないので、その中でも一番係数が単純な選択肢 4 から考えます。
y = xex が正解とします。
y’ = x’ex+x(ex)’
=ex + xex
=(x+1)exです。
微分方程式に代入してみると、左辺 = (x+1)exです。右辺 = (x+1)xex/x
= (x+1)ex です。左辺=右辺です。
以上より、正解は 4 です。

コメント