問 題
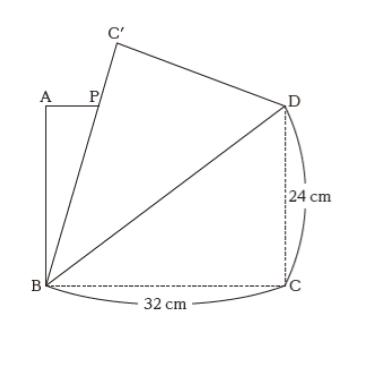
図のように,縦24 cm,横32 cmの長方形ABCD を対角線BD で折って,点Cの移った点を点C’ とする。辺AD と辺BC’ の交点を点P としたとき,線分AP の長さはいくらか。
1 6cm
2 4√3 cm
3 7 cm
4 8 cm
5 5√3 cm
正解 (3)
解 説
AP = x cm とおいて辺の長さを書き込んでみると以下のようになります。
ポイントは、折っているので等しい長さに注目すると CD = C’D = 24cm です。△APB と△C’PD は合同です。直角三角形で一辺の長さと、他の一つの角(∠B が対頂角)で等しいからです。
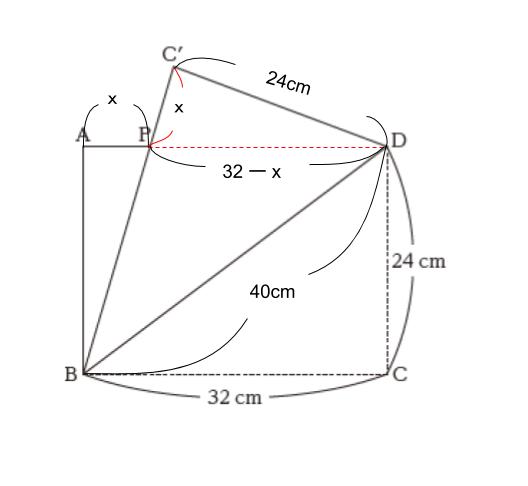
△C’PD に注目して三平方の定理より 242 + x2 = (32-x)2 です。展開して整理すれば 64x = 448 ∴ x = 7 です。以上より、正解は 3 です。
ちなみに、本問では不要ですが、BD は 40 cm です。これは三平方の定理(BD2 = 242+322)でもよいし、直角三角形の辺のよくある比のうちの一つである3:4:5で求めることができます。

コメント