問 題
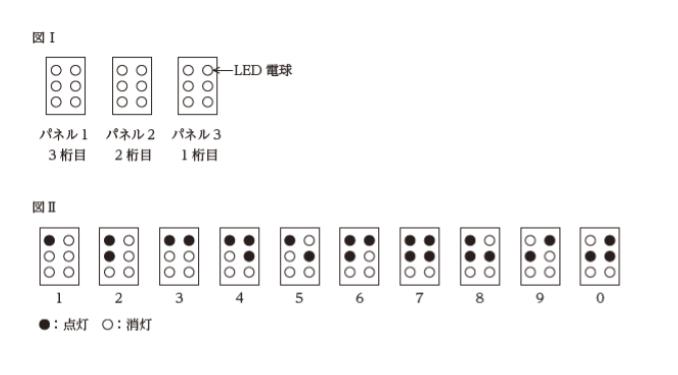
図Ⅰのように, 6 個のLED 電球が取り付けられているパネルが3 枚ある。スイッチを入れると6 個のLED 電球のうち,パネル1 では1 個が,パネル2 では2 個が,パネル3 では3 個がそれぞれ無作為に点灯することが分かっている。
いま,各パネルの点灯状態によって数字を割り当てることとして,図Ⅱのように,各パネルの点灯状態と0 ~ 9 の数字を対応させる。
このとき,スイッチを入れ,パネル1 ,パネル2 ,パネル3を点灯させると, 3 枚全てのパネルに数字が割り当てられて3 桁の数となり,かつ, 3 の倍数となる確率はいくらか。
ただし, 3 枚のパネルの並び順は図Ⅰの状態で固定し,パネルを裏返したり,回転させたりしないものとする。また,各パネルは,図Ⅱに示した点灯状態以外の場合は,数字の割当てがなかったものとする。
1 1/120
2 1/180
3 1/240
4 1/300
5 1/360
解 説
3桁の数になるためには、まず、パネル1で図Ⅱにおける「1」に対応するように、左上が点灯しなければなりません。この確率は、1/6 です。
次に、パネル2で2個点灯した時に、数値が対応するのは、図Ⅱより「2」、「3」、「5」、「9」の4つです。6つの電球のうち2つを点灯する全ての通りは 6C2 = 15 通りです。従って、それぞれの数値に対応する電球が点灯する確率が 1/15 です。
「12?」という3桁の数値で、3 の倍数になるためには、1桁目が 0,3,6,9 である必要があります。3つの電球の点灯と対応する数値が存在するのは「0」か「6」です。この確率は、6つの電球のうち3つを点灯する全ての通りが 6C3 = 20 通りです。よって、0か6に対応する電球が点灯する確率は 2/20 です。
同様に考えていくと
- 「13?」→1桁目は「8」のみ→1/20
- 「15?」→1桁目は「0」か「6」→2/20
- 「19?」→1桁目は「8」のみ→1/20 とわかります。
以上より、もとめる確率は
1/6 × 1/15 × (2/20 + 1/20 + 2/20 + 1/20)
= 1/6 × 1/15 × 6/20
= 6/1800
= 1/300
です。よって、正解は 4 です。

コメント