問 題
次は,統計的検定に関する記述であるが,A,B,Cに当てはまるものの組合せとして最も妥当なのはどれか。
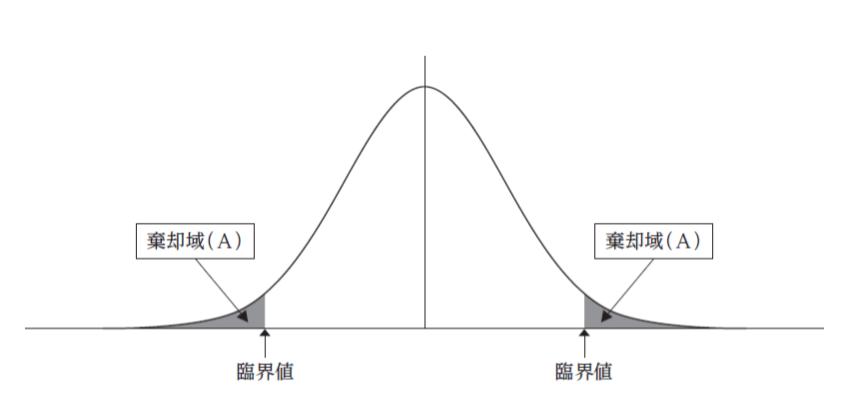
統計的検定では,まず,主張したいこととは逆の「ある二つ以上の条件間に差がない」という帰無仮説を立て,実験などによって得られたデータが,帰無仮説の下では一定の低い確率以下でしか起こり得ない大きな差を示したならば,帰無仮説を棄却し,「差がある」という結論を下す。例えば,有意水準 5 % で両側検定を行う場合,標本分布の左右の裾にそれぞれ A の棄却域を設定し(下図),検定統計量の値が棄却域に入ったら帰無仮説を棄却し,検定統計量の値が採択域に入ったら帰無仮説を採択する。
しかし,仮に帰無仮説が棄却されたとしても,実は帰無仮説が正しい場合もあり,これは誤った判断をしていることになる。そこで,統計的検定では2 種類の誤りを考える。一つは,帰無仮説が真のとき,帰無仮説を棄却してしまう誤りのことで,これを第一種の誤りといい,その確率を a で表す。もう一つは,帰無仮説が偽のとき,帰無仮説を棄却しない誤りのことで,これを第二種の誤りといい,その確率を b で表す。間違っている帰無仮説を正しく棄却できる確率は B であり,これをC という。
A B C
1. 2.5 % 1ーa 信頼水準
2. 2.5 % 1ーa 検定力
3. 2.5 % 1ーb 検定力
4. 5 % 1ーa 信頼水準
5. 5 % 1ーb 検定力
解 説
A ですが
「5% の両側検定」なので、左右の裾にそれぞれ 5 ÷ 2 = 2.5% の棄却域を設定します。
B,C ですが
帰無仮説が偽の時に帰無仮説を棄却しない 第二種の誤りの確率が β なので、1- β で、帰無仮説を正しく棄却します。これを「検定力」と呼びます。ちなみに、信頼水準は、本問では100-有意水準(%)=95%です。
以上より、正解は 3 です。

コメント