公務員試験 H28年 国家一般職(高卒 技術) No.24解説

　問 題　　　　　

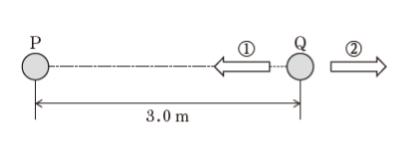
図のように、真空中に固定されている電気量 +1. 0 C の点電荷 P から、3. 0 m 離れた場所に電気量- 2. 0 C の点電荷 Q を置いたとき、この点電荷 Q に働く力の向きと大きさの組合せとして最も妥当なのはどれか。ただし、真空の誘電率を ε₀ とし、1/4πε₀ = 9.0 × 10⁹ とする。

　向き　　大きさ
1.  ①　　1. 5 ×10⁹ N
2.  ①　　2. 0 × 10⁹ N
3.  ①　　6. 0 × 10⁹ N
4.  ②　　2. 0 × 10⁹ N
5.  ②　　6. 0 × 10⁹ N

　解 説　　　　　

まず、正電荷と負電荷という「異符号」の点電荷同士なので「引かれ合い」ます。Pは右に、Qは左に動こうとするはずです。よって、向きは ① です。正解は 1 ~ 3 です。

力の大きさは、２つの点電荷と来たらクーロンの法則です。F_{クーロン力}=kQ₁Q₂/r² です。定数 k が真空中であれば、1/4πε₀ です。Q1、Q2 は、電荷の大きさを示します。r は距離です。本問での数値を代入すれば
F = (9.0 × 10⁹) × 1.0 × 2.0 /(3.0)²
= 2.0 × 10⁹ です。

以上より、正解は 2 です。