問 題
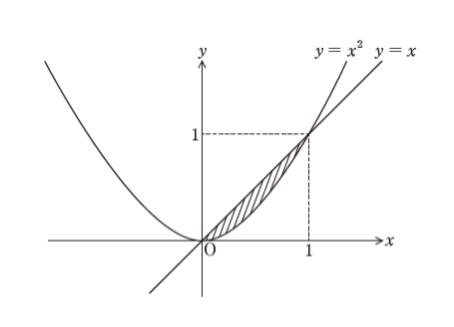
図のように,xy 平面上において曲線 y = x2 と直線 y = x で囲まれた領域の面積として正しいのはどれか。

正解 (1)
解 説
【面積の概算】
明らかに斜線部は面積 1/2 の三角形 のさらに半分よりも小さい面積と概算できます。よって、正解は 1 or 2 です。
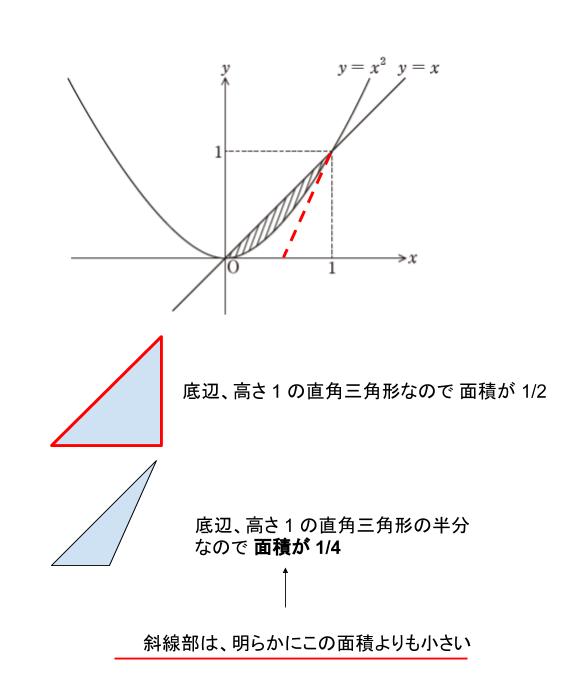
公務員試験では、面積の概算でかなり選択肢が絞れることが多いため、わからない問題でも必ず概算は考慮するとよいです!
【定積分による面積計算】
斜線部は x = 0 ~ 1 において、上端は y = x 、下端は y = x2 に挟まれた部分です。このような部分の面積は ∫ (上ー下)の 定積分で計算することができます。すなわち、求める面積は以下のようになります。
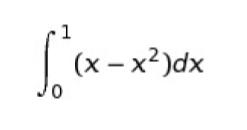
計算すると
[x2/2 ー x3/3]→ 1/2 ー 1/3 = 1/6 です。
以上より、正解は 1 です。
類題 H27no8

コメント