問 題
図のように十分大きな断面積Aをもち、底面部に断面積aの流出口を設けた水槽がある。
この水槽に初期状態で水深Hの水が貯まっているとき、次の記述の㋐、㋑に当てはまるものの組合せとして最も妥当なのはどれか。
ただし、水は完全流体であり、エネルギー損失はないものとする。また、流出口での水脈の縮流は生じないものとする。
なお、重力加速度の大きさをgとする。
「初期水位を原点とし、排水に伴う水位の低下量をhとした場合、単位時間当たりの流出口からの排水量Qは( ㋐ )となる。
このことから、排水開始後の経過時間をt、水深をh(=H-h)とした場合、tとhの関係をグラフで表せば( ㋑ )のようになる。」
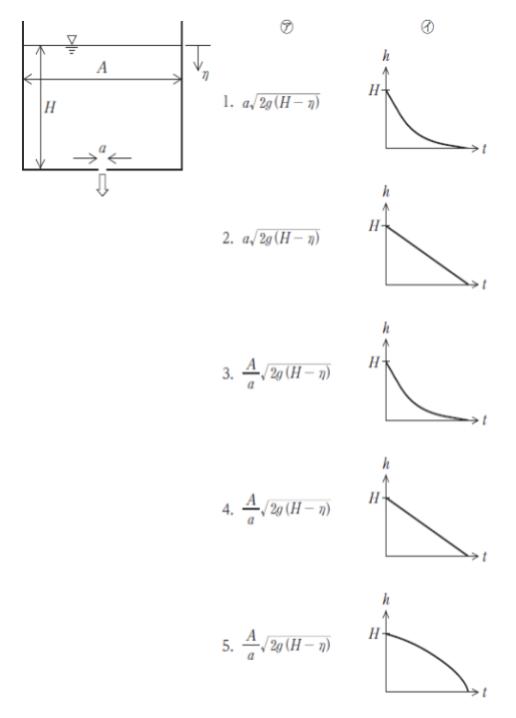
正解 (1)
解 説
㋐について
解法1
トリチェリの定理より
v = √2gh で
h = Hーη なので
正解は 1or2 。
解法2
a = 0 の時、明らかに Q = 0 である。
選択肢 3~5 では a= 0 の時、Q が無限大になるのでだめ。
よって、正解は 1or2
㋑について、水位が下がれば水が抜けにくくなるだろうから、直線ではないと考えられる。
従って、正解は 1 。

コメント