問 題
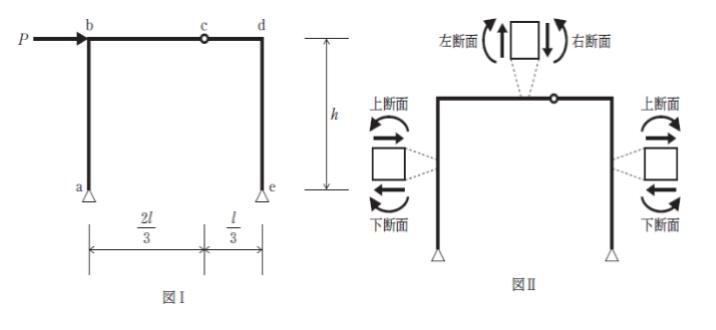
図Ⅰのようなラーメン構造の点bに水平集中荷重が作用しているとき、せん断力図と曲げモーメント図の概形の組合せとして最も妥当なのはどれか。
ただし、点cはヒンジとし、ラーメン構造の自重は無視できるものとする。
また、せん断力と曲げモーメントは図Ⅱの向きを正とする。
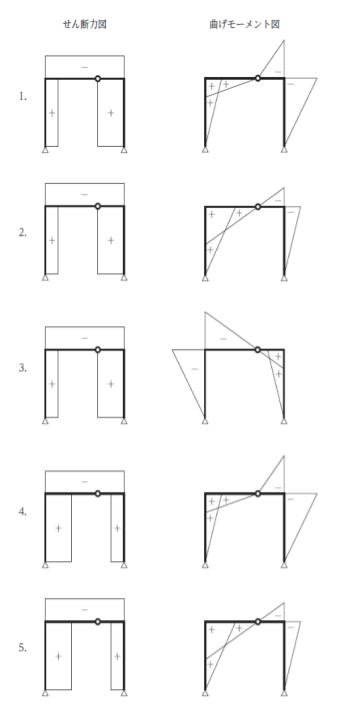
正解 (5)
解 説
まずは支点反力を考えます。C点で切断し、簡単な右側にまず注目します。
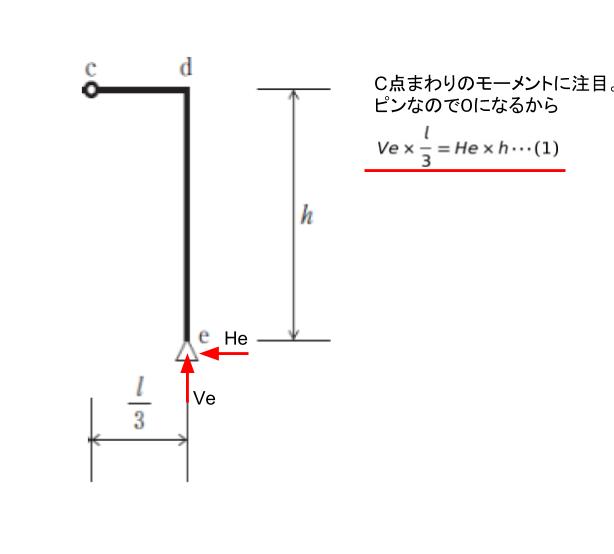
次に、全体の構造に注目します。A点まわりに注目します。固定支点なのでモーメントは0です。

式(1)と式(2)を連立して解きます。
(2)より Ve = P×l/h ・・・(2)’ です。
これを
Ve × l/3 = He × h・・・(1)に代入することで

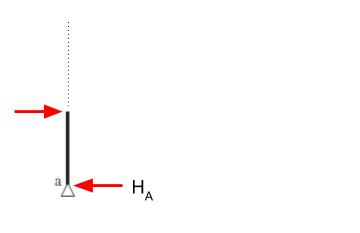
以上により、a 及び e の水平反力がわかりました。すると、ab 間における適当な一点で仮想切断すれば、その点においてHAと逆向きの力がかかっているとわかります。
つまり、せん断力は 2/3P です。
同様に考えれば de 間におけるせん断力は 1/3P です。よって、せん断力の大小関係に注目すれば正解は 4 or 5 です。
モーメントについては「集中荷重がかかる所でないと折れ曲がらない」というルールを知っていれば、ヒンジ部分で曲がっている選択肢 4 が誤りと判断できます。
それを知らなくても点 b 及び点 d で仮想切断しモーメントの大小を考えれば、明らかに b の方が大きいとわかります。
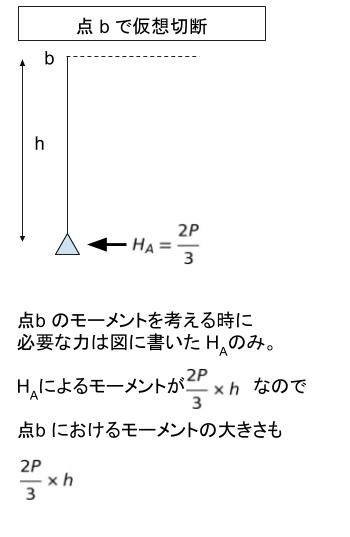
同様に考えれば、点 d で切断した時モーメントの大きさは P/3 × h となります。
モーメントの大きさがb の所でより大きい方が正解です。
よって、選択肢 5 が正解です。

コメント