公務員試験 H28年 国家一般職(土木) No.14解説

　問 題　　　　　

大気中に存在する放射性核種 X₁ は半減期 5.6 × 10³ s で核種 X₂ になる崩壊によって大気中から失われる。

崩壊によって X₁ の個数が時間 t［s］経過後に初めの個数の e^-λt 倍になるとき、λ はおよそいくらか。

ただし、log_e2 = 0.69 とする。

１　1.2 × 10^-4 s^-1

２　2.4 × 10^-4 s^-1

３　3.8 × 10^-4 s^-1

４　5.6 × 10^-4 s^-1

５　8.2 × 10^-4 s^-1

 

 

 

 

 

　解 説　　　　　

X₁ → X₂

半減期 5.6 × 10³ 秒　とのことなので t = 5.6 × 10³ の時、「初めの個数のちょうど半分」=「0.5 倍」になると考えることができます。

問題文より、t 秒後に、初めの個数の e^-λt 倍なので、

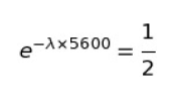
両辺　log_e をとると

ー5600λ = log_e1/2

ここで、右辺 log_e1/2 は以下のように変形できます。

log_e1/2
= log_e1 ー log_e2
= ーlog_e2

これは問題文より ー0.69です。

以上より、

λ = 0.69/5600
= (0.69/0.56) × 10^-4

一番近いのは、選択肢 1 です。