公務員試験 H28年 国家一般職(土木) No.4解説

　問 題　　　　　

定積分

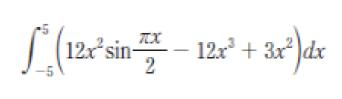
の値はいくらか。

1. 0
2. 24
3. 120
4. 175
5. 250

 

 

 

 

 

　解 説　　　　　

奇関数、つまり f(-x)=-f(x) が成り立つなら、-a ~ a まで積分すると 0 です。従って、結局計算する必要があるのは3x² の項のみです。

よって、正解は 250 です。

すぐに奇関数の積分が思いつかない場合、できる部分から考えるとよいと思われます。

∫3x² → x³ なので定積分を考えると

5³ -((-5)³)
= 125 – (-125)
= 250 です。

∫ー12x³ → －３x⁴ なので定積分を考えると

－３×5⁴ ー（－３×5⁴）= 0 です（！）。

（この時点で「ごちゃごちゃしている第一項も０なら答えは 250 で　選択肢 5 だな。。。」と期待が見えてくるのではないでしょうか。）

x³ のグラフについて考えることで「原点対称の形だったら－５～５みたいに同じ幅積分すればちょうど０」と以下の図のようにイメージできるとよいと思います。

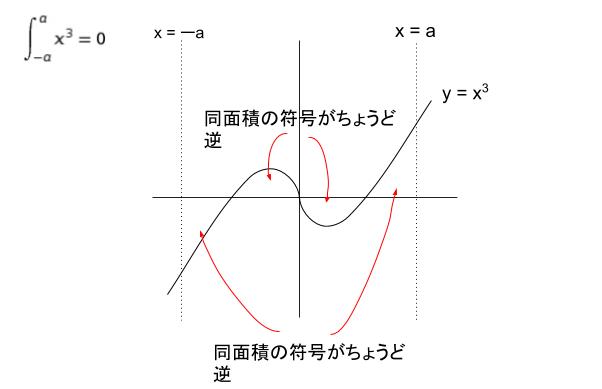
「原点対称」とは「f(-x)=-f(x) が成立」です。x² は、ーｘいれても同じ値です。sin(-x) はーsinx となります。

従って、f(x) = 12x²sin(πx/2) とおくと

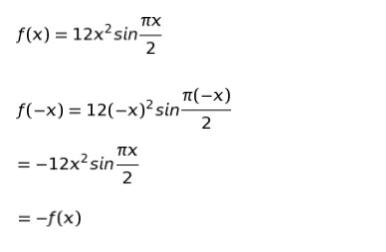
となり、奇関数なので第一項は 0 です。

以上より、250です。

正解は 5 です。