問 題
表Ⅰ は1か月の読書量等に関する調査結果を示したものであるが、これらから確実にいえるのはどれか。なお表 Ⅱ は2013年の調査結果のみが示されている。
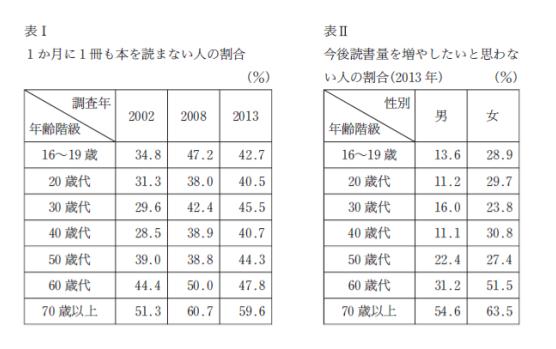
- 三つの調査年の間の変化をみると20歳代以上の各年齢階級について1か月に1冊も本を読まない人の割合は一貫して増大した。
- 三つの調査年のいずれにおいても1か月に1冊も本を読まない人の割合が最大の年齢階級は70歳以上であり最小の年齢階級は40歳代であった。
- 2013年において1か月に1冊も本を読まない人のうち70歳以上の年齢階級には今後読書量を増やしたいと思わない人がいる。
- 2013年において1か月に1冊も本を読まない人の割合が最大の年齢階級と今後読書量を増やしたいと思わない人の割合が最小の年齢階級は一致する。
- 2013年において今後読書量を増やしたいと思わない人の割合の男女差が最大の年齢階級は40歳代でその男女差は19.7%ポイントであった。
解 説
選択肢 1 ですが、表Ⅰの 50 歳代に注目すると、2002 → 2008 で、39.0 → 38.8 と、わずかながら減少しています。よって、選択肢 1 は誤りです。
選択肢 2 ですが、例えば 2008 年は 20歳代が最小です。よって、選択肢 2 は誤りです。
選択肢 3 は、確実です。適当に 70 歳以上を 1000 人と仮定します。70 歳以上の1ヶ月に1冊も本を読まない人は 596 人となります。
今後読書量を増やしたいと思わない人が、男 54.6%,女 63.5% なので、増やしたい人が 男 45.4%、女 36.5% のはずです。70 歳以上の男を x 人とおくと、女は 1000 – x 人です。
よって「読書量を増やしたい人」は、0.454x + 0.365×(1000-x) = 365 + 0.089x と表すことができます。 x は最大でも 1000 なので、365+89 = 454 人までしかありえません。
つまり1ヶ月に1冊も本を読まない596 人のなかには、読書量を増やしたいと思う人が最大でも 454 人しかいないため、最低 142 人は読書量を増やしたいと思わない人がいる、とわかります。
選択肢 4,5 から考えた方が本番ではより簡単と思われます。
選択肢 4 ですが、2013 年の、1月に1冊も本を読まない割合が最大なのは 70 歳以上です。一方、今後読書量を増やしたいと思わない人の割合が最小なのは 30 歳代です。不一致です。よって、選択肢 4 は誤りです。
選択肢 5 ですが、男女差の最大は 60 歳代の 20.3% です。よって、選択肢 5 は誤りです。
以上より、正解は 3 です。

コメント