問 題
ある会議の出席者は10人でいずれも黒青赤の3種類のペンのうち少なくとも1種類を持っている。次のことが分かっているとき確実にいえるのはどれか。
○ 3種類とも持っている人は3人である。
○ 赤のみを持っている人はいない。
○ 黒と青の2種類のみを持っている人がおりその数は黒と赤の2種類のみを持っている人の数と同じである。
○ 青のみを持っている人がおりその数は青と赤の2種類のみを持っている人の数と同じである。
○ 持っている人の数が一番多い種類は青である。
- 黒のみを持っている人はいない。
- 黒を持っていない人は4人である。
- 青を持っている人は7人である。
- 青を持っていない人は1人である。
- 赤を持っている人は5人である。
解 説
黒、赤、青の3種類を持っていたりいなかったりなので、ベン図で考えます。全ての円に含まれない部分については、少なくとも1種類を持っているということなので、考えません。
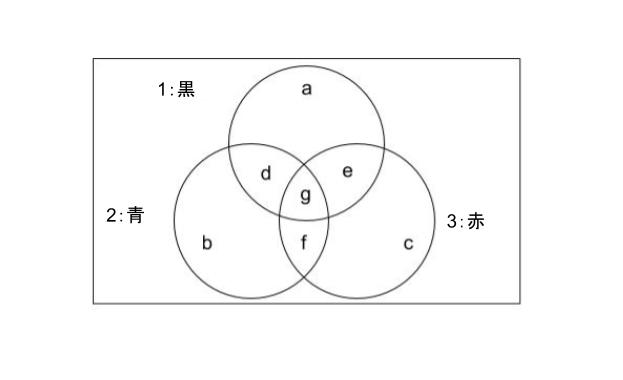
・「会議の出席者が 10 人」→「a + b + c + d + e + f + g = 10」
・「3 種類持っている人が 3 人」→「g = 3」
・「赤のみ持っているのは 0 人」→「c = 0」
・「黒と青 2 種のみと、黒と赤 2 種のみ同じ人数」→「d = e」
・「青のみと、青と赤 2 種のみ同じ」→「b = f」
とまとめることができます。
一番上の式にわかった条件を代入すると
a + b + 0 + d + d + b + 3 = 10 です。
整理すると「a + 2(b + d) = 7」と表すことができます。「 2(b + d) 」という部分に注目すると、b も d も最低 1 なので、a = 1 or 3 です。さらに、「持っている人の数が一番多い種類は、青である」ということから、a = 3 としてしまうと、黒の方が多くなってしまいます。よって、 a = 1 です。
b + d = 3 なので、b = 1, d = 2 か、b = 2, d = 1 です。b = f という条件をふまえ、b ( 「青のみ」)を多くする方がよいと判断して「b = 2, d = 1」と仮定します。すると「a = 1, b = 2, c = 0, d = 1, e = 1, f = 2, g = 3, h = 0」という1例が確定します。
この時、選択肢 1 ですが
「黒のみ」とは、「 a 」です。 a = 1 なので、選択肢 1 は誤りです。
選択肢 2 はOKです。
「黒を持っていない」とは、「b + c + f」です。2 + 0 + 2 = 4 となります。
選択肢 3 ですが
「青を持っている」は「b + d + f + g」です。2 + 1 + 2 + 3 = 8 となります。よって、選択肢 3 は誤りです。
選択肢 4 ですが
「青を持っていない」のは、選択肢 3 より青を持っているのが 8 人なので、10ー8 = 2 です。よって、選択肢 4 は誤りです。
選択肢 5 ですが
「赤を持っている」のは、「c + e + f + g」です。0 + 1 + 2 + 3 = 6 です。よって、選択肢 5 は誤りです。
以上より、正解は 2 です。

コメント