問 題
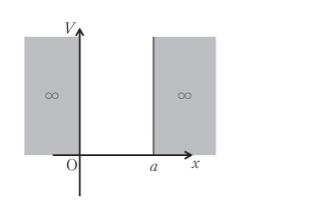
図のように、1 次元の井戸型ポテンシャル中に質量 m の粒子がある。ここで、縦軸の V はポテンシャルエネルギーを表し a は正の定数である。この粒子エネルギー E に関する次の記述の ㋐~㋓ に当てはまるものの組合せとして最も妥当なのはどれか。
「この粒子に対するシュレーディンガー方程式は、h をプランク定数とすると
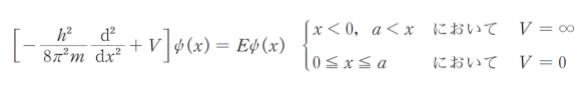
で表される。
x < 0、a < x においては、ψ(x) = ( ㋐ )である。
0 ≦ x ≦ a においては
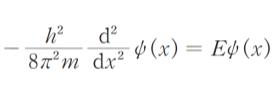
であり、この解を
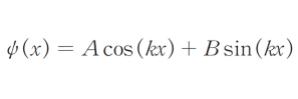
(A、B、kはある実定数)とする。
ここで境界条件から、x = 0 及び x = a で、ψ(x) = ( ㋐ )となる必要がある。これを満たすには、( ㋑ ) = 0、ka = ( ㋒ )(n = 1、2、3、4、…)となる必要がある。このことから、粒子のエネルギーは、E = ( ㋓ )となり、離散的な値をとることが分かる。」
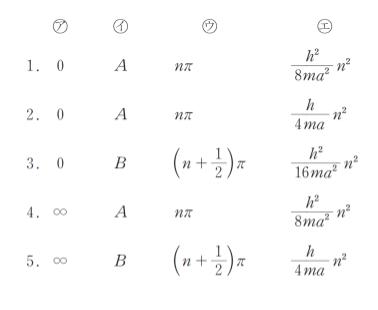
解 説
φ(x) が、粒子が x にいる「確率」を表している という点は知識です。また、ポテンシャルとは位置エネルギーのようなもので、エネルギーが低い方に存在しポテンシャルが ∞ というのはその場所に粒子は存在できない ということです。以上をふまえると、㋐は 0 です。x < 0、 x > a にいる確率は 0 です。
次に、0 ≦ x ≦ a においては、元のシュレディンガー方程式に V = 0 を代入した式がなりたちます。解であるφ(x) を Acos(kx)+Bsin(kx) とおき、φ(0) = 0 でなければいけないので、計算してみると、φ(0) = A です。∵ cos 0 = 1, sin0 = 0 のため。これが 0 なので、A = 0 とわかります。
A = 0 を代入すると、φ(x) は Bsinkx です。さらに、φ(a) = 0 なので、ka = nπ となります。正解は 1 or 2 です。
さて、φ(x) がかなり簡単な形で書けたので、方程式に代入し、二階微分の部分を計算してみます。

選択肢をみると k ではなく n が含まれているので、㋒ の ka = nπより、k = nπ/a を代入して
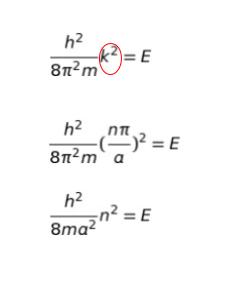
となります。
以上より、正解は 1 です。

コメント