公務員試験 H27年 国家一般職(化学) No.12解説

　問 題　　　　　

炭酸カルシウムの解離反応

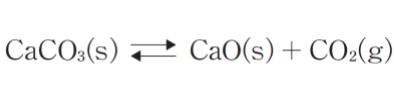
において、固相の活量を 1 とすると、この圧平衡定数 K は CO₂ の平衡分圧 P_CO2 となる(K = P_CO2)。

この解離反応の 1000K 及び 1300K における CO₂ の平衡分圧を測定したところ、それぞれ 5.87 × 10³ Pa、5.41 × 10⁶ Paであった。CO₂ の平衡分圧が 1.00×10⁵ Pa となる温度はおよそいくらか。

ただし、温度を T、圧平衡定数を K、反応エンタルピーを ΔH、気体定数を R とするとこれらには

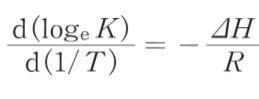
の関係が成り立つ。また、log₁₀5.87 = 0.768、log₁₀5.41 = 0.733とする。

1．1010K
2．1060K
3．1110K
4．1180K
5．1220K

 

 

 

 

 

　解 説　　　　　

CaCO₃ ⇄ CaO + CO₂ で、平衡分圧 = 圧平衡定数となる。とあるので、求めなければいけない「CO₂ の平衡分圧が 1.00 × 10⁵ Paとなる温度」は「圧平衡定数 K が1.00 × 10⁵ となる温度」と読み替えることができます。

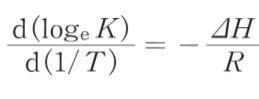
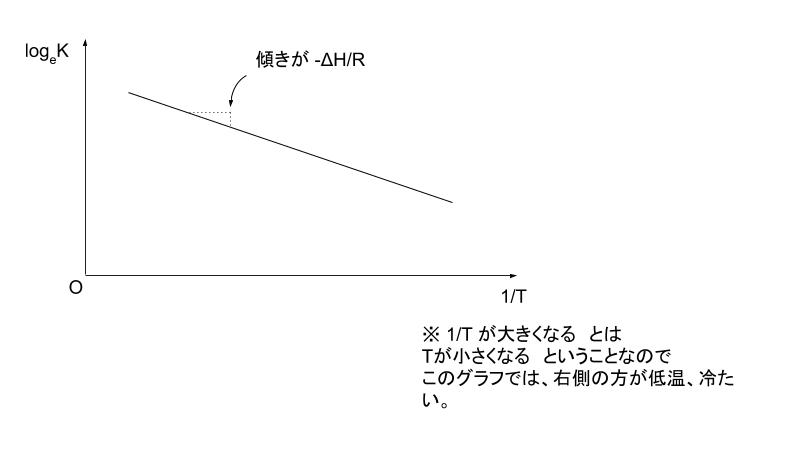
という式から、横軸が 1/T、縦軸が logeK のグラフを考えれば、傾きは右辺の、負の定数（ーΔH/R）ということが読み取れます。

問題文で、1000K ,1300K の CO2 の平衡分圧 = 圧平衡定数 K がそれぞれ与えられているので、1/T,log₁₀K も含めてまとめてみると、以下の表になります。

横軸を 1/T , 縦軸を log₁₀K としたグラフを考えて、わかっている 2 点（T=1000,1300）を書き込むと以下のようになります。

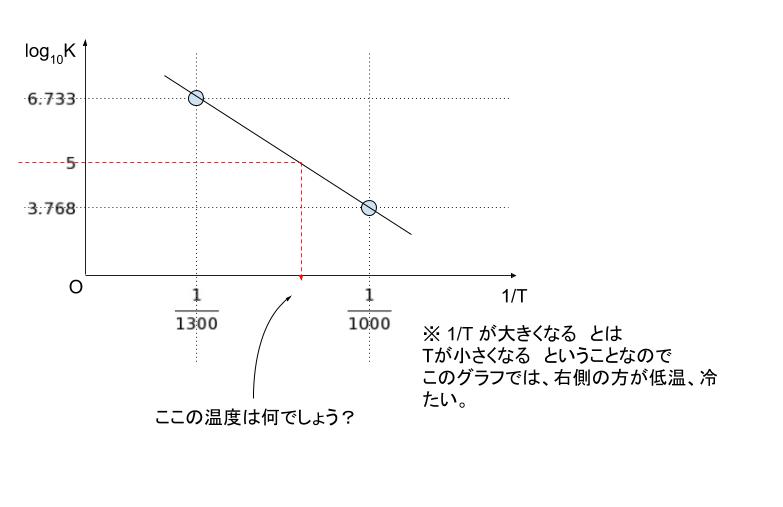5 は、3.768 を下端、6.733 を上端とすれば、「3.768 寄り」なので、真ん中である 1/1150 よりもう少し右、つまり分母が1150 よりも小さくなると考えられます。選択肢から 一番近いのは1/1110 と考えられます。

以上より、正解は 3 です。

ちなみにですが、途中で グラフの縦軸を logeK → log₁₀K に変えています。logeK というのは、結局 log₁₀K/2.3 ぐらいなので、縦軸を log₁₀K にしても全ての 点の y 座標が 下に押し下げられるだけで、結局直線（つまり比例関係）になります。そのため、本問を解く際に影響はありません。