公務員試験 H27年 国家一般職(化学) No.10解説

　問 題　　　　　

実在気体の分子半径に関する、次の記述の㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。ただし、アボガドロ定数を6.0×10²³mol^－1とする。「圧力 P、モル体積 Vm、温度 T の実在気体の状態方程式として

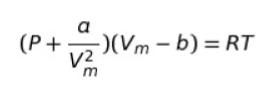
で表されるファンデルワールスの式がある。ここで R は気体定数であり a、bはファンデルワールス定数である。a、bのうち ( ㋐ ) は気体分子 1mol 当たりの排除体積を表している。

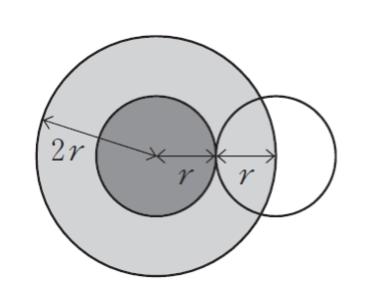
排除体積を分子レベルで考える。気体分子を半径 r の球として考えると、図のように、気体 2 分子において一方の分子の網掛け部分すなわち半径 2r の球の部分より近くには他の分子の中心は侵入できない。つまり他分子を排除している。よって、1 分子当たりにすると、気体分子の体積の( ㋑ )倍が排除体積となる。

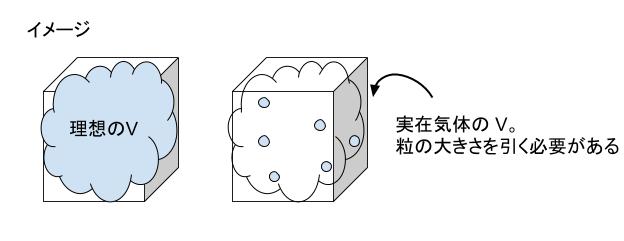
ヘリウムの a、b はそれぞれ 3.45×10^－3 Pa・m⁶・mol^－2 及び 2.37×10^－5 m³・mol^－1 である。ヘリウムの原子半径を r₀〔m〕とすると、r₀³ = ( ㋒ )m³ となる。」

　　㋐　　㋑　　　　　㋒
1．a　　　4　　　3.5×10^－28
2．a　　　8　　　2.4×10^－30
3．b　　　4　　　2.4×10^－30
4．b　　　4　　　1.4×10^－29
5．b　　　8　　　3.5×10^－28

 

 

 

 

 

　解 説　　　　　

【㋐について】
実在気体の体積を調整する項は「ーｂ」です。これは知識です。正解は 1~3 です

【㋑について】
・気体分子の体積 = 半径 r の球の体積 ∴V = 4/3 πr³

・排除体積 = 半径 2r の球の体積 =  4/3 π（2r）³ = 8V（∵V = 4/3 πr³）。気体 2 分子において、排除体積が 8V なので、1 分子あたりでは 4V となります。正解は 3 or 4 です。

【㋒について】
㋐より、b が 1 mol あたりの排除体積と書いてあるので、2.37 × 10^-5 が 「1 mol あたり排除体積」です。

㋑で計算したのが、「1分子あたりの排除体積」なので、１分子あたりなら排除体積は 4V = 4×4/3 πr³ と表すことができています。

1mol = 6.0 × 10²³ 個　なので『2.37×10^-5 = 4×4/3 πr₀³ × (6.0 × 10²³ )』が成り立つはずです。この式を、r₀³ = ・・・の形にすればよいとわかります。選択肢より、それほど厳密な解は不要なので、2.37 ≒ 2.4、 π ≒ 3 と近似して見ると

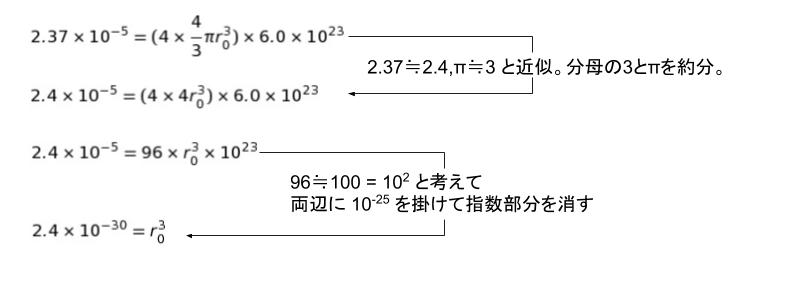となります。

以上より、正解は 3 です。