問 題
半径 R の地球の周りを、地表から R の高さで等速円運動する人工衛星の速さとして最も妥当なのはどれか。ただし、地表における重力加速度の大きさを g とする。
なお、 r 離れた質量 M 及び m の物体間に働く万有引力 F は F = GMm/r2 (Gは万有引力定数)で表される。
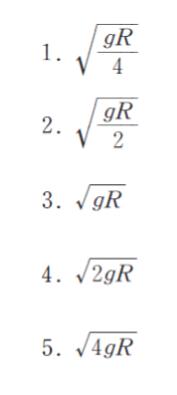
正解 (2)
解 説
万有引力の公式
F = Gm1m2/ r2 は基本公式です。与えられなくても覚えておく方がよいです。※地表面において F = mg であることから、地球の質量を M、地球の半径を R とおけば「GM = gR2」が成り立ちます。万有引力の公式に関連してここまでが基本知識となります。
また、等速円運動ときたので、遠心力の公式を思い出します。「 F遠心力=mrω2 = mv2/r 」です。本問においては、地表から R の高さで円運動をしているから地球と人工衛星の距離は 2R と考えられます。
地球の質量を M、人工衛星の質量を m とします。「等速円運動」しているのだから「万有引力と遠心力が釣り合っている」と読み替えます。それぞれの公式より
GmM/4R2 = mv2/2R となります。以上をまとめると、以下の図のようになります。
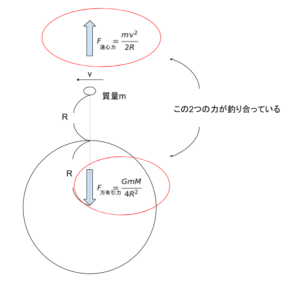
両辺に m,R があるから消して、GM/4R = v2/2。v = ・・・になおせばよさそうだけど、選択肢を見ると、g,R しか残ってはいけない。G,M が邪魔。そこで、地表面における万有引力に関する「GM = gR2 」を使うことで、gR/4 = v2/2∴ v = √(gR/2) となります。
以上より、正解は 2です。

コメント