問 題
ある財の需要曲線と供給曲線がそれぞれ以下のように与えられている。
D = 120- 3p
S = 2p
ただし、D は需要量、Sは供給量、p は価格である。このとき均衡点における需要の価格弾力性 (絶対値) はいくらか。
1. 0.5
2. 1
3. 1.5
4. 2
5. 3
正解 (3)
解 説
需要曲線を p = … に直すと
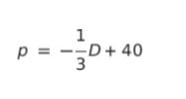
供給曲線を p = … に直すと
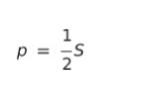
です。
数量を x とおき、横軸を x、縦軸を p としたグラフを考えると、以下のようになります。2つの直線の交点が均衡点です。連立方程式を解いて (x,p) = (48,24) とわかります。
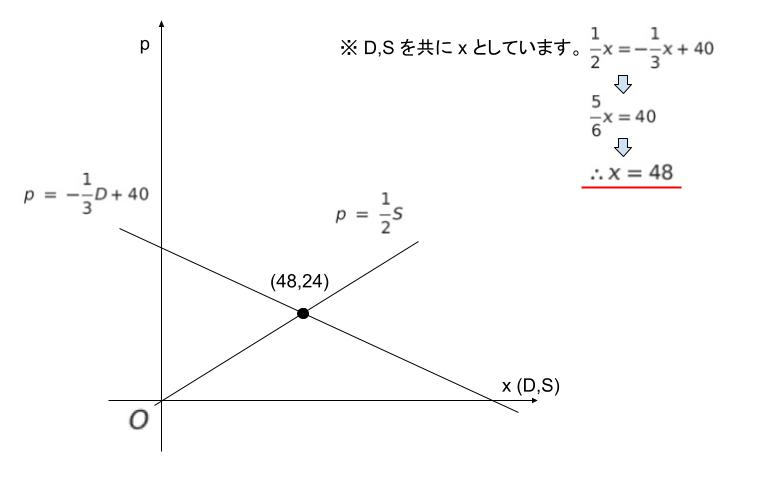
需要の価格弾力性とは、価格が 1% 上昇した時の、需要量の変化率です。均衡点における価格が 24 です。価格 1% の上昇は 0.24 となります。小数でわかりにくいため、整数値の変化となるように、価格を 50% 上昇させ、価格が 12 上昇した場合である、「価格 36」を考えます。すると、p = 36 を代入すれば、D = 120 ー 3 × 36 = 120 ー 108 = 12 です。48 → 12 と減少しているため、需要量は 75% 減少です。
価格 24 → 36 (50% 上昇)、需要量 48 → 12(75% 減少)なので、価格 1% 上昇に対しては、需要量が 1.5% 減少するとわかります。従って、需要の価格弾力性は 1.5 です。
以上より、正解は 3 です。
価格弾力性の定義について、参考 H26 no35

コメント