問 題
家計Aと家計Bの需要曲線が、それぞれ xA = 20- p (ただし、p > 20では xA = 0)、
xB = 40- 5p (ただし、p > 8では xB = 0) で示されているとする。ただし、xA はAの需要量、xB はBの需要量、p は価格である。このときこの二つの家計の需要量を足し合わせた需要量を X としたときの需要関数として正しいのはどれか。ただし、p ≧ 0とする。
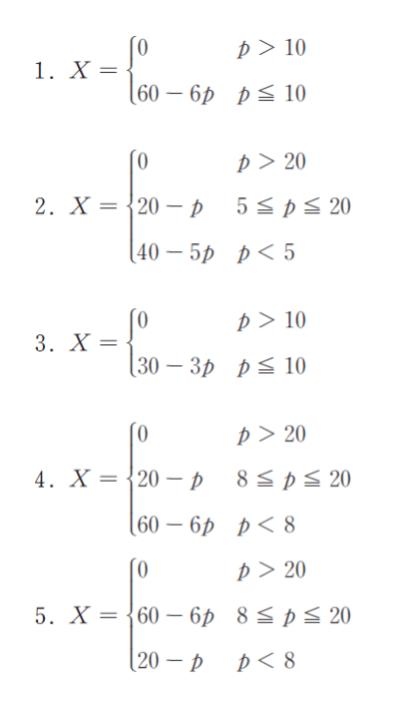
正解 (4)
解 説
p > 8 において、xB = 0 となるため、p > 8 においては、X とは、xA そのものです。従って、8 < p < 20 の時、X = 20 -p です。また、p > 20 で 0 です。選択肢 1 ~ 3 は、p =5 や p = 10 という不自然な場所での場合分けで表されており誤りと考えられます。
選択肢 4,5 に注目します。
選択肢 5 ですが、p < 8 において、xA の式になっているため、誤りです。
以上より、正解は 4 です。

コメント