H27年 国家一般職(高卒 技術) No.3 数学　解説

　問 題　　　　　

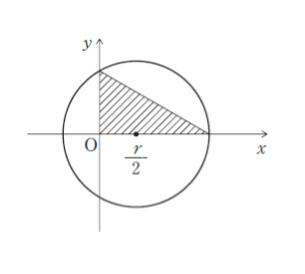
図のような xy 平面上の ( r/2 , 0 ) を中心とする半径 r の円がある。図の斜線部の面積はいくらか。

 

 

 

 

 

　解 説　　　　　

y 軸と円の交点を A、x 軸と円の交点を B とおきます。また、円の中心を O’ とおきます。すると 半径 O’A = r です。⊿ OAO’ に注目すると、「直角三角形の斜辺と、直角を挟む短い方の辺の比が r ： r/2 = 2 : 1」 です。

ここに注目すれば、 辺の比が 1:2:√3 の特殊な直角三角形とわかります。（角度は 90,60,30）。従って、OA = √3r/2 です。

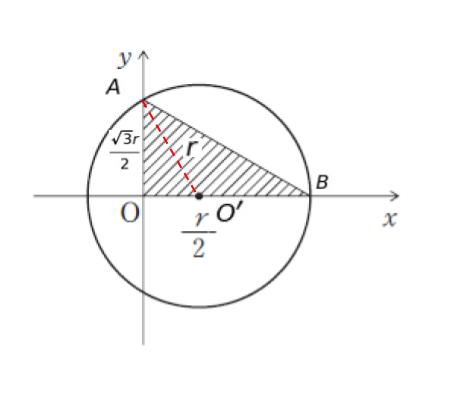
求める斜線部を、△OAO’と△O’BA に分けて面積を考えます。底辺 r/2、高さ √3r/2 の △OAO’ と、底辺 r 、高さ √3r/2 の△ O’BA の面積です。

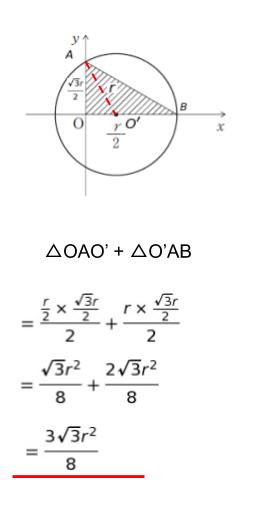
以上より、正解は 4 です。